Question

A piece of string 35 inches long is cut into three smaller pieces along the length of the string. The length of the longest piece is three times the length of the shortest piece. Which one of the following could equal the length of the medium-size piece?
(A) 7
(B) 20
(C) 10
(D) 16

Answer 1

Hint: From the given conditions in question try to make equations for solving value of m.And remember, there can only be one longest and one shortest piece.
Therefore, for checking answers keep the condition \[s < m < l\] in mind.
Where, the length of the longest piece is l, the medium-sized piece is m and the shortest piece is s.

Complete step-by-step answer:
Let us assume the length of the longest piece as l, the medium-sized piece as m and the shortest piece as s, as shown in the figure below:

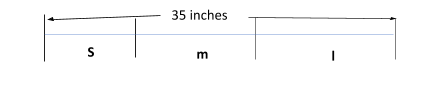
From the question statement, we know that:
The length of the longest piece is three times the length of the shortest piece
 $ \Rightarrow l = 3s $ ---------------[1]
We also know that length of the string is 35 inches
 $ \Rightarrow s + m + l = 35 $ and \[s < m < l\]
 $ \Rightarrow s + m + 3s = 35{\text{ }}\left( {\because l = 3s} \right) $
 $ \begin{gathered}
   \Rightarrow 4s + m = 35 \\
   \Rightarrow s = \dfrac{{35 - m}}{4} - - - - - - - - [2] \\
\end{gathered} $
Now, we plug in the answer choices for m to see in which case the condition \[s < m < 3s\] holds true
Case 1. When m = 7 then,
 $ s = \dfrac{{35 - 7}}{4} = \dfrac{{28}}{4} = 7 $
When we check, for m = 7 the condition \[s < m < 3s\] doesn’t holds true. $ \left( {\because 7 = 7 < 21} \right) $
Also, the length of the shortest piece and middle piece cannot be equal.
Therefore, option A is not correct.
Case 2. When m = 20 then,
 $ s = \dfrac{{35 - 20}}{4} = \dfrac{{15}}{4} = 3.75 $
When we check, for m = 20 the condition \[s < m < 3s\] doesn’t holds true. $ \left( {\because 3.75 < 20 > 11.25} \right) $
Therefore, option B is not correct.
Case 3. When m = 10 then,
 $ s = \dfrac{{35 - 10}}{4} = \dfrac{{25}}{4} = 6.25 $
When we check, for m = 10 the condition \[s < m < 3s\] holds true. $ \left( {\because 6.25 < 10 < 18.75} \right) $
Hence, option C is correct holding onto it.
Case 4. When m = 16 then,
 $ s = \dfrac{{35 - 16}}{4} = \dfrac{{19}}{4} = 4.75 $
When we check, for m = 16 the condition \[s < m < 3s\] doesn’t hold true. $ \left( {\because 4.25 < 16 > 12.75} \right) $
Therefore, option B is not correct.
So, the correct answer is “Option C”.

Note: In this question, it’s not only about finding the length of the medium sized piece; it’s about finding its length in such a way that the SHORTEST and the LONGEST pieces remain themselves. If you only try to find out the length, you will end up falling for the trap answers like B, A and D.