Question

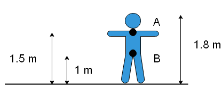
A person wants to see part of his image (see fig). His eye level is at 1.8 m above the ground. If he uses the minimum size of the mirror required for this, find the height of the lowest point of the mirror above the ground.

A) $ 2.4 $
B) $ 7.4 $
C) $ 1.4 $
D) $ 3.4 $

Answer 1

Hint The height of the mirror should be half of the height of the highest point of the object that has to be seen. Since the person wants to see point B in the mirror which is the lowest object, the length of the mirror should be half of the length of the person above point B.

Complete step by step answer
Whenever an object is placed in front of a plane mirror, the mirror size should at least be half of the object size to see the object completely in the mirror.
We’ve been given that a person is standing in front of a mirror and we have to find the height of the lowest point of the mirror.
Now the height of the highest point of the mirror must be such that the person can see the point A in the mirror. So the mirror must be half the distance of the distance AB. So we can calculate the length of the mirror $ h $ as
 $ h = \dfrac{{1.8 - 1}}{2} $ from point B
 $ h = 0.4\,m $
Since we want to find the height of the lowest point of the mirror above the ground, as point B is 1m above the ground, the lowest point of the mirror will at a height $ h' $ such that
 $ h' = 0.4 + 1 $
 $ \Rightarrow h' = 1.4m $
Which corresponds to option (C).

Note
The trick to solving this question is to realize the fact that a properly positioned mirror has to be of a length half of the height of the object. In our case, since the object is above the ground and the person wants to observe the part AB, we should only consider the length of AB to determine the height of the mirror.