Question

A person observes that the full length of a train subtends an angle of $15{}^\circ $. If the distance between the train and the person is $3km$, the length of the train, calculated using parallax method, in meters is?
A $45$
B $45\pi $
C. $250\pi $
D. $75\pi $

Answer 1

Hint: Convert angle subtended by length of train from degrees to radians. Assume length of train as an arc of a circle and calculate it by using relation of angle subtended by arc on centre. The ratio of length of the arc and radius of the circle of which the arc is a part is equal to the angle subtended by the arc, in radians, at centre.

Formula used:
 $\text{Angle (in radians) = }\dfrac{\text{Arc}}{\text{Radius}}$

Complete step by step answer:
Parallax is defined as the difference in apparent position of an object seen along two different lines of sight and is measured as the angle between those two lines of sight.

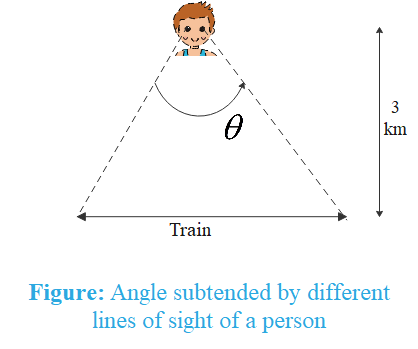
The person observes that the full length of the train subtends an angle of $\theta=15^\circ$.
We convert the angle in radians.
${{180}^{{}^\circ }}=\pi \,rad\Rightarrow {{1}^{{}^\circ }}=\dfrac{\pi }{180}\,rad$
Therefore,
${{15}^{{}^\circ }}=15\times \dfrac{\pi }{180}\,rad=\dfrac{\pi }{12}\,Radian$
We assume that the distance between the person and the train is very much larger than the length of the train. Then, the length of the train can be treated as an arc of the circle with radius as the distance between the train and the person.
Length of an arc of a circle is related to angle subtended by it at centre in radians and its radius as
$\text{Angle (in radians) = }\dfrac{\text{Arc}}{\text{Radius}}$
Substituting the values, we get
$\dfrac{\pi }{12}=\dfrac{\text{Length of the train}}{3km}$
Rearranging and simplifying, we have
Length of the train $=\dfrac{\pi }{12}\times 3000m=250\pi \,m$

The length of the train is $250\pi $ which is option C. Hence, option C is the correct answer.

Note:
Students must learn the basic conversions as these are very handy in solving questions. The ratio of length of the arc and radius of the circle of which the arc is a part is equal to the angle subtended by the arc, in radians, at centre. Astronomers use the parallax method to determine distance between two stars.