Question

A person moves thirty meter north, then twenty meter east and then $30\sqrt 2 $ meter south-west. Evaluate its displacement from the original position.

Answer 1

Hint: Displacement is a vector quantity and it is the shortest distance between the initial and final position of an object during motion.

Complete step-by-step answer:

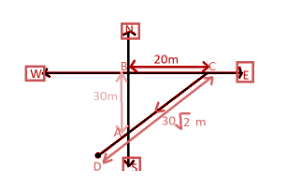
Given that,
Person moves thirty meter north i.e. $AB = 30$ meter
And twenty meter east i.e. $BC = 20$ meter
Then $30\sqrt 2 $meter south west i.e. $CD = 30\sqrt 2 $ meter
Since displacement is the distance between initial and final position of object during motion
Therefore displacement is, $AD = CD - CA$
Here $CD = 30\sqrt 2 $ meter given and in order to calculate $CA$ apply Pythagoras theorem in right angle triangle $ABC$
 $
  \therefore C{A^2} = A{B^2} + B{C^2} \\
  C{A^2} = {30^2} + {20^2} \\
  C{A^2} = 900 + 400 \\
  C{A^2} = 1300 \\
  CA = 36.05 \\
$
As, $AD = CD - CA$
Putting the values we get:
$
  AD = 30\sqrt 2 - 36.05 \\
  AD = 42.42 - 36.05 \\
  AD = 6.37 \\
$
Hence the displacement from the original position is $6.37$ meter.

Note: Here, from the figure displacement is represented by $AD$ which is equal to $CD - CA$, the value of $CD$ is $30\sqrt 2 $meter which is given and in order to calculate $CA$ we applied the Pythagoras theorem in right angle triangle $ABC$and calculated the value of $CA$ as $36.05$ meter, hence the value of $AD$is calculated as $6.37$ meter which represents the displacement.