Question

A person has an 18cm wide face and his two eyes are separated by 8cm. Find the minimum width of a mirror required for the person to view his face laterally.
A. 9cm
B. 4cm
C. 5cm
D. 13cm

Answer 1

Hint: The law of reflection states that the angle of reflection and angle of incidence are equal after reflection from the plane mirror. Using this fact, draw the ray diagram of the image formation of the face in the plane mirror. Use the geometry of the figure to determine the width of the mirror.

Complete answer:
As we can see this question is based on the law of reflection which states that the angle of reflection and angle of incidence are equal after reflection from the plane mirror. Let us discuss the conditions for the minimum width of the mirror. The person must see the right edge of his face from the left eye at the end of the mirror and vice versa for the left edge of the face. Also, the centre of the face and mirror must lie on the perpendicular bisector of the line joining the two eyes.

Now, let us observe the following figure.

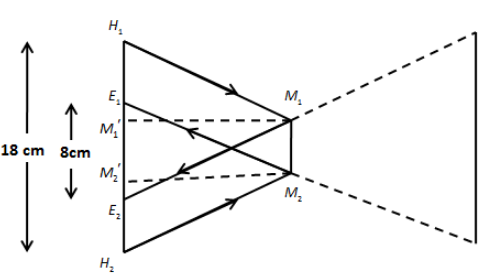
In the above figure, \[{H_1}\] is the left edge of the face and the light reflected from \[{H_1}\] again reflects at the end of the mirror \[{M_1}\] and then enters a right eye at \[{E_2}\]. \[{H_2}\] is the right edge of the face and the light reflected from \[{H_2}\] again reflects at the end of the mirror \[{M_2}\] and then enters a left eye at \[{E_1}\].
Let the distance \[{H_1}{H_2} = D\] and \[{E_1}{E_2} = d\].
From the above ray diagram and law of reflection stated above, we can write,
\[{H_1}{M_1}^\prime = \dfrac{{{H_1}{E_2}}}{2}\] and \[{H_2}{M_2}^\prime = \dfrac{{{H_2}{E_1}}}{2}\] …… (1)

We can write \[{H_1}{E_2}\] as,
\[{H_1}{E_2} = D - \dfrac{1}{2}\left( {D - d} \right)\]
\[ \Rightarrow {H_1}{E_2} = \dfrac{{D + d}}{2}\] …… (2)
Similarly,
\[{H_2}{E_1} = \dfrac{{D + d}}{2}\] …… (3)
We can express the distance \[{M_1}^\prime {M_2}^\prime \] as,
\[{M_1}^\prime {M_2}^\prime = D - {H_1}{M_1}^\prime - {H_2}{M_2}^\prime \]
Using equation (1), (2) and (3) in the above equation, we get,
\[{M_1}^\prime {M_2}^\prime = D - \dfrac{{D + d}}{4} - \dfrac{{D + d}}{4}\]
\[ \Rightarrow {M_1}^\prime {M_2}^\prime = D - \left( {D + d} \right)\left( {\dfrac{1}{4} + \dfrac{1}{4}} \right)\]
\[ \Rightarrow {M_1}^\prime {M_2}^\prime = D - \left( {\dfrac{{D + d}}{2}} \right)\]
\[ \Rightarrow {M_1}^\prime {M_2}^\prime = \dfrac{{D - d}}{2}\]
Substituting \[D = 18{\text{cm}}\] and \[d = 8\,{\text{cm}}\] in the above equation, we get,
\[{M_1}^\prime {M_2}^\prime = \dfrac{{18 - 8}}{2}\]
\[ \therefore {M_1}^\prime {M_2}^\prime = 5\,{\text{cm}}\]
Therefore, the width of the mirror should be 5cm.

So, the correct answer is option C.

Note: For the person to see his whole face in the mirror, the mirror should not necessarily have the same dimensions as that of the face. Since the ray reflected from the end of the mirror is reflected from the other end of the face, we can see the whole face in the mirror which has lower width than the dimensions of the face. The essential step in this solution is the use of the law of reflection.