Question

A particle of mass $2\times {{10}^{-5}}Kg$ moves horizontally between two horizontal plates of a charged parallel plate capacitor between which there is an electric field of 200 N/C acting upward. A magnetic induction of 2.0 T is applied at right angles to the electric field in a direction normal to both B and v. If g is $9.8m/{{s}^{2}}$ and the charge on the particle is ${{10}^{-6}}C$, then find the velocity of charge particle so that it continues to move horizontally.
A: 2m/s
B: 20m/s
C: 0.2 m/s
D:100m/s

Answer 1

Hint: This comes under the application of Lorentz force that is the force which is generated on a charged particle due to the presence of an electric field and a magnetic field. We are given a similar condition here. We can approach this question by keeping the principle of Lorentz force in our minds.

Complete step by step answer:
We are given that
Mass of the particle is $2\times {{10}^{-5}}Kg$
Upward electric field acting on the particle is 200N/C
Magnetic induction is 2.0 T
Charge on the particle is ${{10}^{-6}}C$
Acceleration due gravity is $9.8m/{{s}^{2}}$
We have to find the velocity of the charged particle to maintain the horizontal motion.

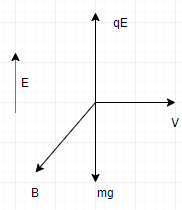
The electric force acting on the particle is \[F=qE={{10}^{-6}}\times 200=2\times {{10}^{-4}}N\]
The weight that acts downwards is $W=mg=2\times {{10}^{-5}}\times 9.8=1.96\times {{10}^{-4}}$
This implies that $F>W$. Hence to make the net force zero, F has to act downwards.
$
F=(2-1.96)\times {{10}^{-4}}=4\times {{10}^{-6}} \\
\implies {{10}^{-6}}\times 2\times v=4\times {{10}^{-6}} \\
\therefore v=2m/s \\
$

So, the correct answer is “Option A”.

Note:
The Lorenz force is best explained using the right hand rule, where the middle finger represents the force, index finger represents the magnetic field and as a result the thumb represents the direction of the current. This method helps the students to find the directions in a simpler way.