Question

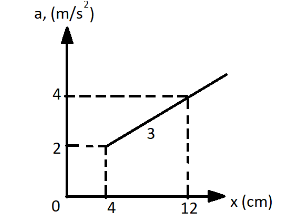
A particle moves along the positive x-axis with an acceleration ${a_x}$ in meter per second squared which increases linearly with x expressed in centimeter, as shown in the graph for an interval of its motion. If the velocity of the particle at $x = 4\;{\text{cm}}$ is $0.40\;{\text{m}}/{\text{s}}$, determine the velocity at $x = 12\;{\text{cm}}$.

A. $0.2\;{\text{m}}/{\text{s}}$
B. $0.4\;{\text{m}}/{\text{s}}$
C. $0.8\;{\text{m}}/{\text{s}}$
D. $1.6\;{\text{m}}/{\text{s}}$

Answer 1

Hint: The above problem is based on the kinematics. The area under the acceleration time graph gives the velocity of the particle. The acceleration is the slope of the velocity time graph. The velocity of the particle is given at some position and velocity at other points can be found by calculating the area of the given graph.

Complete step by step answer:
Given: The initial position of the particle is ${x_1} = 4\;{\text{cm}} = 4\;{\text{cm}} \times \dfrac{{1\;{\text{m}}}}{{100\;{\text{cm}}}} = 0.04\;{\text{m}}$.
The initial velocity of the particle is $u = 0.40\;{\text{m}}/{\text{s}}$.
The final position of the particle is ${x_2} = 12\;{\text{cm}} = 12\;{\text{cm}} \times \dfrac{{1\;{\text{m}}}}{{100\;{\text{cm}}}} = 0.12\;{\text{m}}$.
The initial acceleration of the particle is ${a_1} = 2\;{\text{m}}/{{\text{s}}^2}$.
The final acceleration of the particle is ${a_2} = 4\;{\text{m}}/{{\text{s}}^2}$.
The expression for the area of the acceleration of the graph is given as
$A = \dfrac{1}{2}\left( {{a_1} + {a_2}} \right)\left( {{x_2} - {x_1}} \right)......\left( 1 \right)$
The area under the curve in the integral form is given as:
$A = \int\limits_u^v {vdv} $
$\Rightarrow A = \left( {\dfrac{{{v^2}}}{2}} \right)_u^v$
$\Rightarrow A = \dfrac{{{v^2}}}{2} - \dfrac{{{u^2}}}{2}......\left( 2 \right)$
Equate the expression (1) and expression (2) to find the final velocity of the particle.
$\dfrac{{{v^2}}}{2} - \dfrac{{{u^2}}}{2} = \dfrac{1}{2}\left( {{a_1} + {a_2}} \right)\left( {{x_2} - {x_1}} \right)$
$\Rightarrow{v^2} = {u^2} + \left( {{a_1} + {a_2}} \right)\left( {{x_2} - {x_1}} \right)$
$\Rightarrow v = \sqrt {{u^2} + \left( {{a_1} + {a_2}} \right)\left( {{x_2} - {x_1}} \right)} ......\left( 3 \right)$
Substitute $0.04\;{\text{m}}$for ${x_1}$, $0.12\;{\text{m}}$for ${x_2}$, $2\;{\text{m}}/{{\text{s}}^2}$ for ${a_1}$, $4\;{\text{m}}/{{\text{s}}^2}$ for ${a_2}$ and $0.40\;{\text{m}}/{\text{s}}$for u in the expression (3) to find the final velocity of the particle.
$\Rightarrow v = \sqrt {{{\left( {0.40\;{\text{m}}/{\text{s}}} \right)}^2} + \left( {2\;{\text{m}}/{{\text{s}}^2} + 4\;{\text{m}}/{{\text{s}}^2}} \right)\left( {0.12\;{\text{m}} - 0.04\;{\text{m}}} \right)} $
$\therefore v = 0.8\;{\text{m}}/{\text{s}}$

Thus, the velocity of the particle at $12\;{\text{cm}}$is $0.8\;{\text{m}}/{\text{s}}$ and the option (c) is the correct answer.

Note:The above problem can also be solved by using the third equation of the motion. The third equation of the motion is given as ${v^2} = {u^2} + 2ax$. Convert the value of position from centimeter to meter before substituting in the formula.