Question

A particle is moving with a speed of $10{\text{m}}{{\text{s}}^{ - 1}}$ parallel to the x-axis starting from $\left( {0,2{\text{m}}} \right)$ . Find the angular speed of the particle about the origin at $t = 0 \cdot 2{\text{sec}}$.
A) $2 \cdot 5{\text{rad}}{{\text{s}}^{ - 1}}$
B) $5{\text{rad}}{{\text{s}}^{ - 1}}$
C) $2{\text{rad}}{{\text{s}}^{ - 1}}$
D) None of these

Answer 1

Hint:Here the particle can be considered to be executing rotational motion about the origin. So the radius of the circle will be the coordinate of the given starting point of the particle. The angular speed and the linear speed of a particle are related. The conservation of angular momentum can be applied to obtain the angular velocity at the given time.

Formulas used:
-The angular velocity of a particle is given by, $\omega = \dfrac{v}{r}$ where $v$ is the linear velocity of the particle and $r$ is the radius of the circle described by the particle.
-The angular momentum of a particle is given by, $L = mvr$ where $m$ is the mass of the particle, $v$ is its linear velocity and $r$ is the radius of the circle described by the particle.

Complete step by step answer.
Step 1: Sketch a rough figure describing the motion of the particle and list the parameters given in the question.

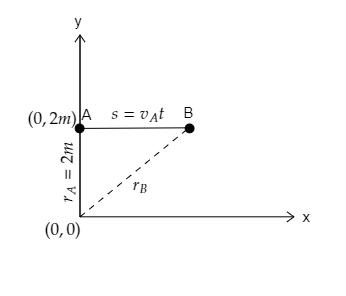
In the above figure, the starting point of the particle is marked by A and B represents the position of the particle after the given time.
The radius of the path described by the particle at A will be ${r_A} = 2{\text{m}}$ .
The velocity of the particle at A is given to be ${v_A} = 10{\text{m}}{{\text{s}}^{ - 1}}$ .
The time taken to reach B is given to be $t = 0 \cdot 2{\text{s}}$ . The particle covers a distance $s = {v_A}t = 10 \times 0 \cdot 2 = 2{\text{m}}$ during that time.
Let ${v_B}$ be the linear velocity of the particle at B.
The radius at B will be ${r_B} = \sqrt {{r_A}^2 + {s^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 {\text{m}}$
Step 2: Based on the conservation of angular momentum at points A and B, obtain the linear velocity at B.
At A and B, the angular momentum of the particle will be conserved.
$ \Rightarrow {L_A} = {L_B}$ -------- (1)
The angular momentum at A is expressed as ${L_A} = m{v_A}{r_A}$ ---------- (2) where $m$ is the mass of the particle.
Substituting for ${v_A} = 10{\text{m}}{{\text{s}}^{ - 1}}$ and ${r_A} = 2{\text{m}}$ in equation (2) we get, ${L_A} = m \times 10 \times 2 = 20m$ .
Thus the angular momentum at A is ${L_A} = 20m$ .
The angular momentum at B will be ${L_B} = m{v_B}{r_B}$ ---------- (3)
Substituting for ${r_B} = 2\sqrt 2 {\text{m}}$ in equation (3) we get, ${L_B} = m{v_B} \times 2\sqrt 2 = 2\sqrt 2 m{v_B}$ .
Thus the angular momentum at B is ${L_B} = 2\sqrt 2 m{v_B}$ .
Now substituting for ${L_A} = 20m$ and ${L_B} = 2\sqrt 2 m{v_B}$ in equation (1) we get, $20m = 2\sqrt 2 m{v_B}$
$ \Rightarrow {v_B} = \dfrac{{20}}{{2\sqrt 2 }} = \dfrac{{10}}{{\sqrt 2 }}{\text{m}}{{\text{s}}^{ - 1}}$
Thus the velocity of the particle at B is ${v_B} = \dfrac{{10}}{{\sqrt 2 }}{\text{m}}{{\text{s}}^{ - 1}}$ .
Step 3: Express the relation for the angular velocity of the particle and make necessary substitutions.
The angular velocity of the particle at B is given by, ${\omega _B} = \dfrac{{{v_B}}}{{{r_B}}}$ -------- (4)
Substituting for ${v_B} = \dfrac{{10}}{{\sqrt 2 }}{\text{m}}{{\text{s}}^{ - 1}}$ and ${r_B} = 2\sqrt 2 {\text{m}}$ in equation (4) we get, ${\omega _B} = \dfrac{{10}}{{\sqrt 2 \times 2\sqrt 2 }} = 2 \cdot 5{\text{rad}}{{\text{s}}^{ - 1}}$
Thus the angular speed of the particle at the given time is ${\omega _B} = 2 \cdot 5{\text{rad}}{{\text{s}}^{ - 1}}$ .

So the correct option is A.

Note:The origin will act as the centre of the circular path described by the particle at both points A and B. So the distance from the origin to the points A and B are the radii of the circular paths. The triangle formed by the distance $s$ , the radius ${r_A}$ and the radius ${r_B}$ is a right triangle. So we employed Pythagoras theorem to obtain the hypotenuse ${r_B}$ which gives ${r_B}^2 = {r_A}^2 + {s^2}$ .