Question

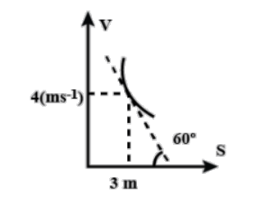
A particle is moving along a straight line whose velocity-displacement graph is shown in Figure. What is the acceleration when the displacement is 3m?

A. $8\sqrt 3 \,m{s^{ - 2}}$
B. $3\sqrt 3 \,m{s^{ - 2}}$
C. $\sqrt 3 m{s^{ - 2}}$
D. $4\sqrt 3 m{s^{ - 2}}$

Answer 1

Hint:As, the question we have referred to the figure to start with the solution. As, tangent to the curve makes an angle $60^\circ $ with the x-axis in clockwise direction, so we have to subtract $60^\circ $ from $180^\circ $ and the angle that tangent makes with the x-axis is $120^\circ $.
The tangent to the curve is the slope of the graph, with the help of this we will get to know the value of $\dfrac{{dv}}{{ds}}$, which will help us to find the value of acceleration, as $a = \dfrac{{dv}}{{dt}}$, which can be simplified as $a = \left( {\dfrac{{dv}}{{ds}}} \right)\dfrac{{ds}}{{dt}}$, by this we can find the value of acceleration.

Complete Step by Step Answer:
Given, the tangent to the curve is making a an angle $60^\circ $ in clockwise direction with respect to x-axis and $\dfrac{{ds}}{{dt}} = 3$, as we have to find the acceleration when the particle has displaced $3\,m$.
As, the slope of the graph is measured from the anti-clockwise sense(direction) from the x-axis, i.e., the angle is taken from the anti-clockwise sense(direction) from the x-axis.
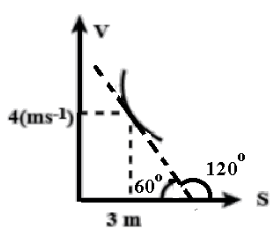
Consider, the figure given in the question, as the slope makes an angle of $60^\circ $ from clockwise sense(direction), so $180^\circ - 60^\circ = 120^\circ $, from anticlockwise sense(direction)
The slope of the v-s curve is defined by $\dfrac{{dv}}{{ds}}$.
So, $\dfrac{{dv}}{{ds}} = \tan 120^\circ = - \sqrt 3 $.
It is quite obvious the value of $\dfrac{{dv}}{{ds}}$ will be negative as the curve is having a negative slope and also when the distance is increasing the velocity is decreasing.
As, velocity is equal rate of change of displacement, i.e., $v = \dfrac{{ds}}{{dt}}$.
The rate of change of velocity is equal to acceleration, i.e., $a = \dfrac{{dv}}{{dt}}$.
So,
$a = \dfrac{{dv}}{{dt}}$, where we can expand $\dfrac{{dv}}{{dt}}$ as $\dfrac{{dv}}{{dt}} = \left( {\dfrac{{dv}}{{ds}}} \right)\dfrac{{ds}}{{dt}}$.
So,
$
a = \dfrac{{dv}}{{dt}} \\
\Rightarrow a = \left( {\dfrac{{dv}}{{ds}}} \right)\dfrac{{ds}}{{dt}} \\
\Rightarrow a = - \sqrt 3 \left( 3 \right) \\
\Rightarrow a = - 3\sqrt 3 \,m{s^{ - 2}} \\
$
Here, the negative sign indicates that the particle is de-accelerating or having retardation.
Therefore, when the body is displaced by $3\,m$, then the acceleration of the particle is $3\sqrt 3 \,m{s^{ - 2}}$.

Note:This is a question of kinematics, where the displacement is given and we need the find the acceleration, here the tangent to the curve gives slope of the curve which will help us to get the value of the $\dfrac{{dv}}{{ds}}$, and by this we can find the value acceleration as $a = \left( {\dfrac{{dv}}{{ds}}} \right)\dfrac{{ds}}{{dt}}$.
Whenever, the value of acceleration comes out to be negative that means the body is de-accelerating.