Question

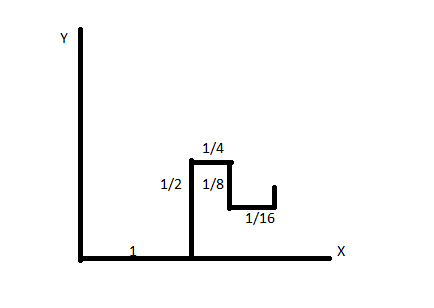
A particle begins at the origin and moves successively in the following manner as shown. $1$ unit to the right. $\dfrac{1}{2}$ unit up. Unit to the right. $\dfrac{1}{4}$ unit down. $\dfrac{1}{{16}}$ to the right etc. the length of each move is half. The length of the previous move and movement continues in a zigzag manner indefinitely. The coordinate of the point to which the zigzag converges is

$(A)\dfrac{4}{3},\dfrac{2}{3}$
$(B)\dfrac{4}{3},\dfrac{2}{5}$
$(C)\dfrac{3}{2},\dfrac{2}{3}$
$(D)2,\dfrac{2}{5}$

Answer 1

Hint: If the number of the terms in the GP is finite then the GP is called the infinite GP.
To calculate the common ratio, divide the second term of the sequence with the first term.
The infinite GP doesn’t have the last term. In this infinite GP when the common ratio is greater than 1 then the series will be larger

Complete answer:
Along x-direction, the distance is the sum of \[1,\dfrac{1}{4},\dfrac{1}{{16}}\]... (common ratio=\[\dfrac{1}{4}\])..so on by adding this infinite GP, we get \[x{\text{ }} = {\text{ }}\dfrac{{1{\text{ }}}}{{\left( {1 - \left( {\dfrac{1}{4}} \right)} \right)}} = {\text{ }}4/3.\]
Similarly, along y, the movement is as \[ + {\text{ }}\dfrac{1}{2},\dfrac{{ - 1}}{8},\dfrac{{ + 1}}{{32}}\]..... so this GP of common ratio (-\[\dfrac{1}{4}\]) adds up to
 \[y = {\text{ }}\dfrac{{\dfrac{1}{2}{\text{ }}}}{{\left( {1 - \left( { - \dfrac{1}{4}} \right)} \right)}} = {\text{ 2}}/5.\]
In other ways,
Consider x-axis
\[S{\text{ }} = {\text{ }}1 + \dfrac{1}{4}{\text{ }} + {\text{ }}\dfrac{1}{{16}} + \ldots \]
It is an infinite GP with \[a{\text{ }} = {\text{ }}1\] and \[r{\text{ }} = {\text{ }}1/4\]
\[S{\text{ }} = {\text{ }}1/\left( {1 - 1/4} \right)\]
Hence it becomes,
\[ = \dfrac{4}{3}\]
From this the x coordinate is \[ = \dfrac{4}{3}\]
By Considering the y axis
\[S' = \dfrac{1}{2}-{\text{ }}\dfrac{1}{8}{\text{ }} + {\text{ }}\dfrac{1}{{32}}\]-…
Now It is an infinite GP with \[a = \dfrac{1}{2}\] and \[\;r = - \dfrac{1}{4}\]
Now the equation becomes,
\[S{\text{ }} = {\text{ }}\dfrac{{\left( {\dfrac{1}{2}} \right)}}{{\left( {1 + \dfrac{1}{4}} \right)}}\]
\[ = \dfrac{2}{5}\]
So, y coordinate \[ = \dfrac{2}{5}\]
 The zigzag converging point is \[\left( {\dfrac{4}{3},\dfrac{2}{3}} \right)\]
Hence option (B) is the answer.

Note: Finally, The zigzag converging point is \[\left( {\dfrac{4}{3},\dfrac{2}{3}} \right)\]
The G.P is the geometric progression that contains the non-zero numbers.
Infinite geometric series is calculated by the sum of the infinite geometric sequence.