Question

A parallel plate capacitor of capacitance C has spacing d between two plates having area A.
The region between the plates is filled with N dielectric layers, parallel to its plates, each with N dielectric layers, parallel to its plates, each with thickness \[{{\delta = }}\dfrac{{{d}}}{{{N}}}\]. The dielectric constant of the \[{{{m}}^{{{th}}}}\]s layer is \[{{{K}}_{{m}}} = {{K}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)\]. For a very large N\[\left( { > {{10}^3}} \right)\], the capacitance C is\[{{\alpha }}\left( {\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{dln2}}}}} \right)\].
The value of \[\alpha \]will be ……………………………. [\[{{{\varepsilon }}_{{0}}}\]is the permittivity of free space]

Answer 1

Hint: To find the required value for α we have to understand the region between the plates having N dielectric layers is equivalent to combination N-capacitors having different values of dielectric constant. So, we have to calculate the small elemental capacitance for each capacitor in a sequent manner and then take their equivalent capacitance. We take the formula for an elemental capacitor as:- \[{{dc = }}\dfrac{{{{{\varepsilon }}_{{0}}}{{{K}}_{{m}}}{{A}}}}{{{{dx}}}}\] , where \[{{dc }}\]is the elemental capacitance dx is the spacing between plates having elemental area A. Then after we will calculate the equivalent capacitance by the formula: \[\dfrac{1}{{{{{C}}_{{{eq}}}}}} = \int {\dfrac{1}{{{{dc}}}}} \] and get the required value for α.

Complete step by step answer:
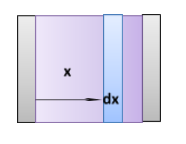
To calculate the elemental capacitance we are taking small elemental capacitor at a distance x of dielectric thickness dx along with the spacing of the plate as shown in figure 1.1
Formula used: \[{{dc = }}\dfrac{{{{{\varepsilon }}_{{0}}}{{{K}}_{{m}}}{{A}}}}{{{{dx}}}}\], where \[{{dc }}\]is the elemental capacitance dx is the spacing between plates having elemental area A.

As per the information given in the question we have given that-

\[{{\delta = }}\dfrac{{{d}}}{{{N}}}\]……………. (i)
\[{{{K}}_{{m}}} = {{K}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)\]………. (ii)
\[{{C = \alpha }}\left( {\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{dln2}}}}} \right)\]………….(iii)

\[ \Rightarrow \dfrac{x}{m} = \dfrac{d}{N}\]……………… (iv)
For the series combination of dielectrics formula used:
\[\dfrac{1}{{{{{C}}_{{{eq}}}}}} = \int {\dfrac{1}{{{{dc}}}}} \]………………… (v)
Since, \[\dfrac{{{1}}}{{{{dc}}}}{{ = }}\dfrac{{{{dx}}}}{{{{{k}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}\]
\[ \Rightarrow \dfrac{{{1}}}{{{{dc}}}}{{ = }}\dfrac{{{{dx}}}}{{{{{k}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}\]…………… (vi)
Substitute the value of \[\dfrac{1}{{{{dc}}}}\]in the equation (v), we get
\[\dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_0^d {\dfrac{{{{dx}}}}{{{{{K}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}} \]…………….. (vii)
Using the equation (iii) in equation (vii)
\[ \Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{dx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)}}} \]
\[ \Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{dx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{1 + }}\dfrac{x}{d}} \right)}}} \]
\[ \Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{ddx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{d + x}}} \right)}}} \]

\[ \Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\dfrac{{{d}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}\ln 2\]
\[ \Rightarrow {{{C}}_{{{eq}}}}{{ = }}\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{d}}\ln 2}}\]……………….. (viii)
On comparing both the equation (viii) and (ii), we get
\[\alpha = 1\]

$\therefore$ The value of $\alpha = 1$


Note:
In order to answer this type of question, the key is to know the basic algorithm behind the calculation of equivalent capacitance of a system having dielectric varies with certain parameters like varies with distance, varies with filling orientation, etc. So for grasping the ideas behind such conceptual problems one should have to practice a lot of numerical and derivative type problems on this topic.