Question

A parallel plate capacitor made of two plates of length L, width w and separated by distance d. An electric slab (dielectric constant K) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force $F=-\dfrac{\partial U}{\partial x}$ where U is the energy of the capacitor when dielectric inside the capacitor up to distance x (see figure). If the charge on the capacitor is Q then the force on the dielectric when it is near the edge is:

Answer 1

Hint: First of all, we will find the net capacitance between two parallel plates by calculating the capacitance when the dielectric slab travelled x distance and also where the slab is not present by using the formula of capacitance in relation with area and distance between slabs. Then from this we will find the energy of the capacitor by using the formula of energy in relation with capacitance and charge on the body and then taking its differentiation with respect to x we will find the value of force.
Formula used:
$C=k\dfrac{{{\varepsilon }_{0}}A}{d}$, $U=\dfrac{{{Q}^{2}}}{2C}$

Complete answer:
in question we are given that a slab is present at the end of the dielectric parallel plate capacitor and it is dragged between the plates by force F, which acts due to charge of capacitor and we are to find that force F acting on the slab as shown in the figure,

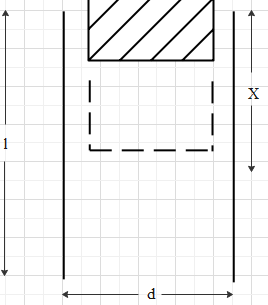
 Now, we know that capacitance of a parallel plate capacitor can be given by the formula,
$C=k\dfrac{{{\varepsilon }_{0}}A}{d}$
Where, C is capacitance, k is dielectric constant ${{\varepsilon }_{0}}$ is electrostatic constant, d is distance between plates and A is area of plates.
now, let the distance travelled by slab is x, so we will find the capacitance of the capacitor due to slab at distance x which can be given as,
$C=k\dfrac{{{\varepsilon }_{0}}A}{d}$

Where A can be given as $wx$, where w is the width of the slab and x will be length equal to the distance it travelled. On, substituting we will get,

$C=k\dfrac{{{\varepsilon }_{0}}\left( wx \right)}{d}$ ……………………..(i)
Now, capacitance of capacitor where slab is not present can be given as,
$C=\dfrac{{{\varepsilon }_{0}}\left( w\left( l-x \right) \right)}{d}$ …………………..(ii)
As, value of k is equal to 1 if slab is not present and the area becomes $w\left( l-x \right)$.
Now, the net capacitance can be given as,
$C'=\dfrac{{{\varepsilon }_{0}}\left( w\left( l-x \right) \right)}{d}+\dfrac{k{{\varepsilon }_{0}}\left( wx \right)}{d}$
$C'=\dfrac{{{\varepsilon }_{0}}w}{d}\left( l+\left( k-1 \right)x \right)$ …………………..(iii)
Now, the energy of capacitor can be given as,
$U=\dfrac{{{Q}^{2}}}{2C}$
Where, U is energy, Q is charge of plate and C is capacitance of plate. So, on substituting the value of C from expression (iii) we will get,
$\Rightarrow U=\dfrac{{{Q}^{2}}}{2\dfrac{{{\varepsilon }_{0}}w}{d}\left( l+\left( k-1 \right)x \right)}$
$\Rightarrow U=\dfrac{{{Q}^{2}}d}{2{{\varepsilon }_{0}}w\left( l+\left( k-1 \right)x \right)}$ ……………..(iv)
Now, the force acting on the slab is given by the expression $F=-\dfrac{\partial U}{\partial x}$ in the question, so, now we will substitute the value of U from expression (iv) and we will get,
$F=-\dfrac{\partial }{\partial x}\left( \dfrac{{{Q}^{2}}d}{2{{\varepsilon }_{0}}w}\dfrac{1}{\left( l+\left( k-1 \right)x \right)} \right)$
On taking partial differentiation with respect to x, we will get,
$F=\dfrac{{{Q}^{2}}d}{2{{\varepsilon }_{0}}w{{l}^{2}}}\left( k-1 \right)$
Thus, the force acting can be given as, $F=\dfrac{{{Q}^{2}}d}{2{{\varepsilon }_{0}}w{{l}^{2}}}\left( k-1 \right)$

Note:
While considering the partial derivation of any quantity, all the other quantities which are in multiplication to the variable are considered as constant so, only the variable with respect to which we are deriving gets derived. This must be kept in mind by students while performing partial derivation otherwise they might make some mistakes and answers will not come.