Question

A parallel plate capacitor is made of two square plates of side ‘a’, separated by a distance d(d << a). The lower triangular portion is filled with a dielectric of dielectric constant K. Find the capacitance of the capacitor.

Answer 1

Hint: Integrating cross-sectional areas using elemental parameters will reveal the whole area with actual parameters. Integration of capacitance of a cross-sectional area of a parallel plate capacitor over the whole area will help to determine the total capacitance of the parallel plate capacitor.

Formula used: For a parallel plate capacitor,
$C=\dfrac{K\text{ }{{\varepsilon }_{0}}a}{d}$
Here,
$K$ is the relative permittivity of the dielectric medium
$\text{ }{{\varepsilon }_{0}}$ is the permittivity of free space
$a$ is the area of the plates
$d$ is the distance between the plates

Complete step by step answer:
In this tricky question, it is important to approach by taking a small cross-sectional area of the parallel plate capacitor. We need to find the capacitance of the cross-sectional area first. Then, we integrate the calculated capacitance over the whole area to determine the total capacitance of the parallel plate capacitor. The figure given below will give a clear picture of the whole idea.

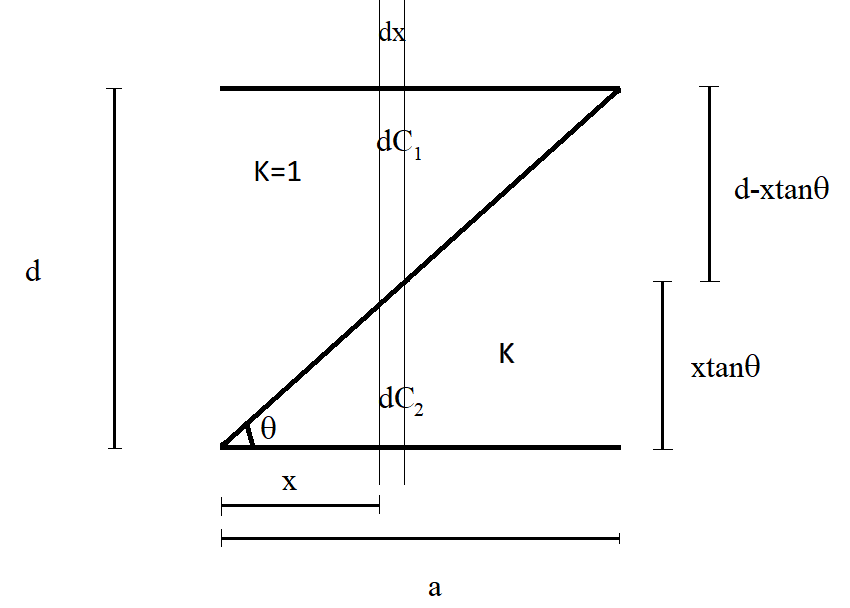
From the figure, it can be understood that the two plates of the parallel plate capacitor are separated by a distance $d$ and that the area of each plate is $a$. The upper half triangle is free space with $K=1$ and the lower half triangle is filled with a dielectric of dielectric constant $K$. We have taken a small cross-sectional area at a distance $x$ from one of the ends of the capacitor. Let one of the angles of the lower half triangle with the dielectric be $\theta $. The length of the cross-sectional area is $dx$ and the elemental area of the same is $adx$. The cross-sectional area of the parallel plate capacitor can be considered as two capacitors $d{{C}_{1}}$ and $d{ C }_{ 2 }$ connected in series. It is clear from the figure that $d{ C }_{ 1 }$ is present in the region where $K=1$ and $d{ C }_{ 2 }$ is present in the region where $K=K$. It is also clear that the length of $d{{C}_{1}}$ is equal to $d-x\tan \theta $ and the length of $d{{C}_{2}}$ is $x\tan \theta $. Now, we have to find the total capacitance of the cross-sectional area of the capacitor. Let us call this capacitance $dC$. Both the capacitors $d{ C }_{ 1 }$ and $d{ C }_{ 2 }$ are connected in series. When capacitors are joined in series, we have the relation: $\dfrac{1}{dC}=\dfrac{1}{d{{C}_{1}}}+\dfrac{1}{d{{C}_{2}}}$
Applying the formula for capacitance to both $d{ C }_{ 1 }$ and $d{ C }_{ 2 }$, we have:
$d{{C}_{1}}=\dfrac{\text{ }{{\varepsilon }_{0}}(adx)}{d-x\tan \theta }$
$d{{C}_{2}}=\dfrac{K{{\varepsilon }_{0}}(adx)}{x\tan \theta }$
Substituting these values in the above equation, we have:
\[\begin{align}
  & \dfrac{1}{dC}=\dfrac{1}{d{{C}_{1}}}+\dfrac{1}{d{{C}_{2}}} \\
 & \dfrac{1}{dC}=\dfrac{d-x\tan \theta }{{{\varepsilon }_{0}}adx}+\dfrac{x\tan \theta }{K{{\varepsilon }_{0}}adx} \\
 & \dfrac{1}{dC}=\dfrac{1}{{{\varepsilon }_{0}}adx}\left( d-x\tan \theta +\dfrac{x\tan \theta }{K} \right) \\
 & \dfrac{1}{dC}=\dfrac{1}{K{{\varepsilon }_{0}}adx}\left( Kd-Kx\tan \theta +x\tan \theta \right) \\
 & \dfrac{1}{dC}=\dfrac{1}{K{{\varepsilon }_{0}}adx}\left( Kd+x\tan \theta (1-K) \right) \\
 & dC=\dfrac{K{{\varepsilon }_{0}}adx}{Kd+x\tan \theta (1-K)} \\
\end{align}\]
This is the capacitance of the cross-sectional area of the parallel plate capacitor. In order to obtain the total capacitance of the parallel plate capacitor, we have to integrate the above equation over the whole area of each plate. This is shown below:
\[\begin{align}
  & \int\limits_{0}^{a}{dC}=C=\int\limits_{0}^{a}{\dfrac{K{{\varepsilon }_{0}}adx}{Kd+x\tan \theta (1-K)}} \\
 & \int\limits_{0}^{a}{\dfrac{K{{\varepsilon }_{0}}adx}{Kd+x\tan \theta (1-K)}}=K{{\varepsilon }_{0}}a\int\limits_{0}^{a}{\dfrac{dx}{Kd+x\tan \theta (1-K)}}=\left. K{{\varepsilon }_{0}}a\dfrac{\ln \left| x\tan \theta (1-K)+Kd \right|}{\tan \theta (1-K)} \right|_{0}^{a} \\
\end{align}\]
The integration is of the form: \[\int{\dfrac{dx}{Ax+B}=\dfrac{1}{A}\ln \left| Ax+B \right|}\]
Simplifying further, we have:
\[\begin{align}
  & \left. \dfrac{K{{\varepsilon }_{0}}a}{\tan \theta (1-K)}\ln \left| x\tan \theta (1-K)+Kd \right| \right|_{0}^{a}=\dfrac{K{{\varepsilon }_{0}}a}{\tan \theta (1-K)}\left\{ \ln \left| a\tan \theta (1-K)+Kd \right|-\ln \left| Kd \right| \right\}=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\left\{ \ln \left| d(1-K)+Kd \right|-\ln \left| Kd \right| \right\} \\
 & \dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\left\{ \ln \left| d(1-K)+Kd \right|-\ln \left| Kd \right| \right\}=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\{\ln \left| d \right|-\ln \left| Kd \right|\}=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln \left( \dfrac{d}{Kd} \right) \\
\end{align}\]
since we know that \[\ln A-\ln B=\ln \dfrac{A}{B}\]. Also note that \[\tan \theta =\dfrac{d}{a}\]
On further simplification, we have:
\[\begin{align}
  & \dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln \left( \dfrac{d}{Kd} \right)=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln \left( \dfrac{1}{K} \right) \\
 & \dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln \left( \dfrac{1}{K} \right)=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln ({{K}^{-1}})=-\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(1-K)}\ln (K)=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(K-1)}\ln (K) \\
\end{align}\]
Therefore, the total capacitance of the parallel plate capacitor, \[C=\dfrac{K{{\varepsilon }_{0}}{{a}^{2}}}{d(K-1)}\ln (K)\]

So, the correct answer is “Option C”.

Note: Students should understand that this is a tricky question. The idea of taking values for cross-sectional areas and finally integrating them over the whole needs to be remembered in such questions. Students need to be well aware of integral as well as natural logarithmic formulas. It is also important to notice that the final answer can be rearranged in different ways to match the correct answer given in the options.