Question

A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be

A. $400\% $
B. $66.6\% $
C. $33.3\% $
D. $200\% $

Answer 1

Hint: Whenever the gap between a capacitor is filled with a dielectric material, the capacitance increases by a constant known as the dielectric constant of the medium. However, when it is half-filled, we have to consider the serial combination of the capacitance without the dielectric and with the dielectric.

Complete answer:
It is given that a parallel plate capacitor has a capacitance C. It is half filled with a dielectric of dielectric constant 5. We need to find the percentage increase in the capacitance.
That capacitance of a capacitor is given by equation
$C = \dfrac{{{\varepsilon _0}A}}{d}$
Where, ${\varepsilon _0}$ is the permittivity of free space, A is the area and $d$ is the distance between the plates of the capacitor.
In the presence of a dielectric the equation for capacitance is given as
$C = \dfrac{{{\varepsilon _0}kA}}{d}$
Where k is the dielectric constant.
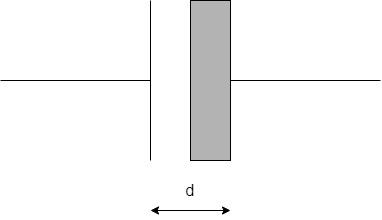
The dielectric is only half filled as shown:

Thus, we can consider this as two capacitors connected in series, one having air as a dielectric medium and the other having the material with dielectric constant 5.
The initial capacitance is
$C = \dfrac{{{\varepsilon _0}A}}{d}$
The dielectric constant of air is one. Since the distance between the capacitors is half-filled, the actual distance to be filled is, $\dfrac{d}{2}$.
After inserting dielectric, the capacitance of part having air is
$ \Rightarrow {C_a} = \dfrac{{{\varepsilon _0}A}}{{\dfrac{d}{2}}}$
Since the area is only half the initial area.
$ \Rightarrow {C_a} = \dfrac{{2{\varepsilon _0}A}}{d}$
The capacitance of the part with dielectric medium is
$ \Rightarrow {C_d} = \dfrac{{{\varepsilon _0}kA}}{{\dfrac{d}{2}}}$
$ \Rightarrow {C_d} = \dfrac{{10{\varepsilon _0}A}}{d}$
The net capacitance is the series combination of the capacitances ${C_a}$ and ${C_d}$ which is given by the formula –
$\dfrac{1}{{C'}} = \dfrac{1}{{{C_a}}} + \dfrac{1}{{{C_d}}}$
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{d}{{2{\varepsilon _0}A}} + \dfrac{d}{{10{\varepsilon _0}A}}$
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{{5d + d}}{{10{\varepsilon _0}A}}$
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{{6d}}{{10{\varepsilon _0}A}}$
$\therefore C' = \dfrac{{10{\varepsilon _0}A}}{{6d}} = \dfrac{{5{\varepsilon _0}A}}{{3d}}$
This is the final capacitance.
Now let us calculate the percentage increase.
Percentage increase can be calculated as
$\Delta C{\text{ = }}\dfrac{{C' - C}}{C} \times 100$
$ \Rightarrow \Delta C{\text{ = }}\dfrac{{\dfrac{{5{\varepsilon _0}A}}{{3d}} - \dfrac{{{\varepsilon _0}A}}{d}}}{{\dfrac{{{\varepsilon _0}A}}{d}}} \times 100$
$ \Rightarrow \Delta C{\text{ = }}\dfrac{{\dfrac{{5{\varepsilon _0}A - 3{\varepsilon _0}A}}{{3d}}}}{{\dfrac{{{\varepsilon _0}A}}{d}}} \times 100$
$ \Rightarrow \Delta C{\text{ = }}\dfrac{{\dfrac{{2{\varepsilon _0}A}}{{3d}}}}{{\dfrac{{{\varepsilon _0}A}}{d}}} \times 100$
$ \Rightarrow \Delta C{\text{ = }}\dfrac{2}{3} \times 100 = 66 \cdot 66\% $
Thus, the percentage increase in capacitance is 66.66 %.

So, the correct answer is option B.

Note:
If the dielectric material is filled in the entire distance but only, half the area of the plates, we have to consider it as a parallel combination. The net capacitance in the parallel combination is equal to the algebraic sum of the individual capacitances.