Question

A parallel beam of light of wavelength $500{\text{nm}}$ falls on a narrow slit and the resulting diffraction pattern is observed on a screen $1{\text{m}}$ away. It is observed that the first minimum is at a distance of $2 \cdot 5{\text{mm}}$ from the centre of the screen. Find the width of the slit.

Answer 1

Hint: As the given slit is narrow, the position of the first minimum in the single-slit diffraction experiment will be proportional to the wavelength of the light used, the distance between the screen and the slit and it will be inversely proportional to the width of the slit.

Formula Used:
The position of the ${{\text{n}}^{{\text{th}}}}$ minima in a single slit diffraction experiment is given by, ${y_n} = \dfrac{{n\lambda D}}{d}$ where $\lambda $ is the wavelength of the light used, $D$ is the distance between the screen and the slit and $d$ is the width of the slit.

Complete step by step answer:
Step 1: Sketch a figure of the arrangement and list the parameters given.

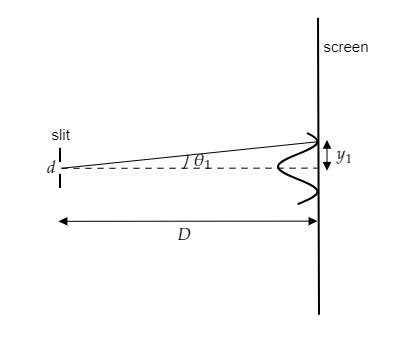
The distance between the screen and the slit is given to be $D = 1{\text{m}}$ .
The position of the first minimum from the centre of the screen is given to be ${y_1} = 2 \cdot 5{\text{mm}}$ .
The wavelength of the light used is given to be $\lambda = 500{\text{nm}}$ .
Let $d$ be the width of the slit which is to be determined.
Step 2: Express the relation for the position of the first minimum of the diffraction pattern to determine the width of the slit.
The position of the ${{\text{n}}^{{\text{th}}}}$ minima in a single slit diffraction experiment is given by,
${y_n} = \dfrac{{n\lambda D}}{d}$ --------- (1)
For the first minimum, we have $n = 1$, then equation (1) becomes, ${y_1} = \dfrac{{\lambda D}}{d}$
$ \Rightarrow d = \dfrac{{\lambda D}}{{{y_1}}}$ -------- (2)
Substituting for $\lambda = 500 \times {10^{ - 9}}{\text{m}}$, $D = 1{\text{m}}$ and ${y_1} = 2 \cdot 5 \times {10^{ - 3}}{\text{m}}$ in equation (2) we get, $d = \dfrac{{500 \times {{10}^{ - 9}} \times 1}}{{2 \cdot 5 \times {{10}^{ - 3}}}} = 2 \times {10^{ - 4}}{\text{m}}$
Thus the width of the slit will be $d = 0 \cdot 2{\text{mm}}$ .

Note: While substituting the values of physical quantities in any equation, make sure that all the quantities are expressed in their respective S.I. units. If this is not the case, then the necessary conversion of units must be done. Here the wavelength of the light and the position of the first minimum are converted to meters as $\lambda = 500 \times {10^{ - 9}}{\text{m}}$ and ${y_1} = 2 \cdot 5 \times {10^{ - 3}}{\text{m}}$ respectively before substituting in equation (2).