Question

A parallel beam of light is incident from air at an angle \[\alpha \] on the side PQ of a right angled triangular prism of a refractive index \[\eta = \sqrt 2 \]. Light undergoes total internal reflection in the prism at the face PR when \[\alpha \] has a minimum value of \[{45^o}\]. The angle \[\theta \] of the prism is:

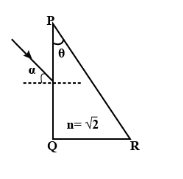
A. \[{15^o}\]
B. \[{22.5^o}\]
C. \[{30^o}\]
D. \[{45^o}\]

Answer 1

Hint – In questions we should remember the laws of refraction and specially the Snell’s law i.e.
${n_1}\sin \alpha = {n_2}\sin \beta $, where \[\alpha \] is angle of incidence and $\beta $ is angle of refraction.

Formula used-
1) ${n_1}\sin \alpha = {n_2}\sin \beta $
2) Angle sum of a triangle is ${180^o}$

Complete step-by-step answer:
The ray will bend toward the normal since it goes from the rarer to denser medium and then strikes with the face PR and then TIR happens.

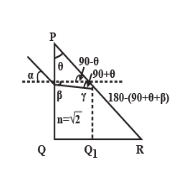
Given, \[\eta = \sqrt 2 \]

${\alpha _{\min }} = {45^o}$

We know that, ${n_1}\sin \alpha = {n_2}\sin \beta $

$1 \times \sin \alpha = n \times \sin \beta $

When the value of ${\alpha _{\min }} = {45^o}$and \[\eta = \sqrt 2 \].

Then the value of $\sin \beta = \dfrac{1}{2}$
Therefore the value of\[\beta = {30^o}\]

Here the new term \[\delta \] is called the angle of deviation. It is defined as the difference of the angle between refraction and the incidence angle and this angle is made when there is a minimum two mediums of different refractive index as here it is air and glass.

\[\delta = 90 - (180 - (90 + \theta + \beta ))\]

∴ Applying Snell's law at surface PR we get the equation as:

\[
  \therefore \sqrt 2 \sin \delta = 1 \\
  \therefore \sin (\theta + \beta ) = \dfrac{1}{{\sqrt 2 }} \\
  \theta + \beta = {45^o} \\
  \theta + {30^o} = {45^o} \\
  Therefore,\theta = {15^o} \\
\]

Hence, the correct option is A.

Note: In this question we should use Snell's law of refraction and basic geometry of triangles to find the angle as the sum of angles of a triangle is ${180^o}$. Doing this will solve your problem. Generally these types of problems arise from this chapter. So, learning the important formulas will be a better option for students.