Question

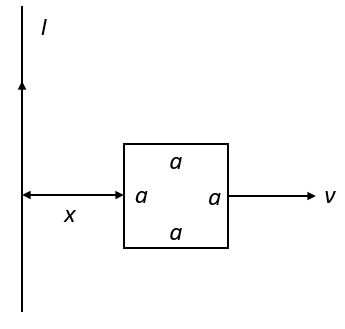
(A) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in fig.
(B) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, \[v = 10\,m/s\]. Calculate the induced emf in the loop at the instant when \[x = 0.2\,m\]. Take \[a = 0.1\,m\] and assume that the loop has a large resistance.

Answer 1

Hint: Calculate the magnetic flux associated with the small vertical strip of the square loop and then integrate this magnetic flux from $x$ to \[x + a\]. The magnetic flux in the square loop is equal to mutual inductance of the square loop times the current flowing through the wire.

Formula used:
\[B = \dfrac{{{\mu _0}I}}{{2\pi r}}\]

Here, B is the magnetic field, I is the current, and r is the distance between the wire and square loop.

\[\varepsilon = BLv\]

Here, L is the length of the side of the loop and v is the velocity of the loop.

Complete step by step answer:We know that the magnetic field due to current carrying wire at a distance r from the wire is,
\[B = \dfrac{{{\mu _0}I}}{{2\pi r}}\] …… (1)

Here, I is the current flowing through the long straight wire.

Now, consider the strip of small width \[dr\] at a distance r from the current carrying wire. The magnetic flux associated with the small strip of width \[dr\] is,
\[d\phi = BdA\] …… (2)

Here, dA is the area of the small strip dr.

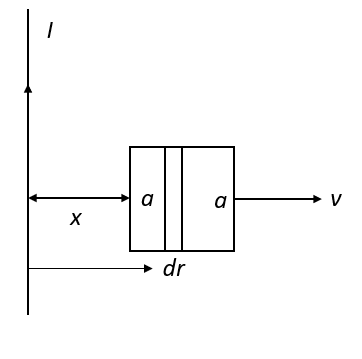
Substitute equation (1) in equation (2).
\[d\phi = \left( {\dfrac{{{\mu _0}I}}{{2\pi r}}} \right)\left( {a\,dr} \right)\]

Integrate the above equation from x to \[x + a\], to determine the total flux associated with the square loop.
\[\phi = \int\limits_x^{x + a} {\left( {\dfrac{{{\mu _0}I}}{{2\pi r}}} \right)\left( {a\,dr} \right)} \]
\[ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\int\limits_x^{x + a} {\dfrac{1}{r}dr} \]
\[ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}r} \right]_x^{x + a}\]
\[ \Rightarrow \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}\left( {x + a} \right) - {{\log }_e}\left( x \right)} \right]\]
\[ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}\left( {\dfrac{{x + a}}{x}} \right)} \right]\]

We know the relation between magnetic flux and mutual inductance,
\[\phi = MI\]
\[ \Rightarrow M = \dfrac{\phi }{I}\]

Substitute the value of magnetic flux in the above equation.
 \[M = \dfrac{{\dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}\left( {\dfrac{{x + a}}{x}} \right)} \right]}}{I}\]
\[\therefore M = \dfrac{{{\mu _0}a}}{{2\pi }}\left[ {{{\log }_e}\left( {\dfrac{{x + a}}{x}} \right)} \right]\]

This is the expression for the mutual inductance between the current carrying wire and square loop of side a.


(B)

The expression for induced emf in the loop due to current carrying wire is,
\[\varepsilon = BLv\] …… (3)

Here, L is the length of the side of the loop and v is the velocity of the loop.

The magnetic field due to current carrying wire at a distance x from the wire is,
\[B = \dfrac{{{\mu _0}I}}{{2\pi x}}\]

Substitute the above equation in equation (3).
\[\varepsilon = \left( {\dfrac{{{\mu _0}I}}{{2\pi x}}} \right)lv\]

Substitute 50 A for I, \[4\pi \times {10^{ - 7}}\] for \[{\mu _0}\], 0.2 m for x, 0.1 m for l and 10 m/s for v in the above equation.
 \[\varepsilon = \left( {\dfrac{{4\pi \times {{10}^{ - 7}} \times 50\,A}}{{2\pi \times 0.2\,m}}} \right)\left( {0.1\,m} \right)\left( {10\,m/s} \right)\]
\[ \Rightarrow \varepsilon = 5 \times {10^{ - 5}}\,V\]

Therefore, the induced emf in the loop is \[5 \times {10^{ - 5}}\,V\].

Note:To calculate the total flux associated with the square loop, integrate the magnetic field from x to \[x + a\] and not from 0 to \[x + a\]. The unit of emf and voltage is the same and it is volt.