Question

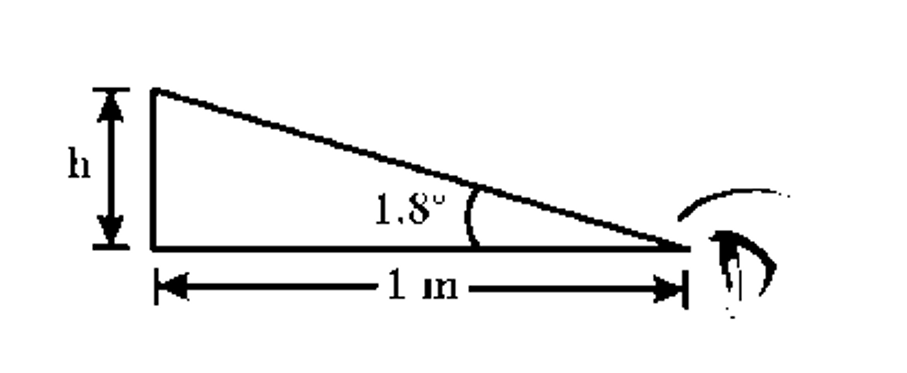
A normal eye can see an object making an angle of \[{1.8^o}\] at the eyes. What is the approximately height of object which can be seen by an eye placed as a distance of 1m from the object:

Answer 1

Hint: In such questions when given angles are very small then there are certain assumptions from which you can relate the situation in the given problem. Don’t get misconceptions about this question and do not try to solve such questions with the usual trigonometric formula, you may get wrong answers in such situations like using \[\tan \theta \] in this case.

Complete step by step answer:
There are several approximations that you can make over some trigonometric functions.
These are:
\[\sin \theta \approx \theta \]
\[\tan \theta \approx \theta \]
\[\cos \theta \approx 1 - \dfrac{{{\theta ^2}}}{2} \approx 1\]
Now according to question the best suitable formula is
\[\tan \theta \approx \theta \]
$\Rightarrow$ \[\tan \theta = \dfrac{P}{B}\]
$\Rightarrow$ \[\theta = {18^o}\]
$\Rightarrow$ \[\tan \theta = \theta = {(1.8)^o} = \dfrac{P}{B}\]
$\Rightarrow$ \[\dfrac{h}{1} = 1.8\]
Thus, h = 1.8m.

Note: There are a number of ways to demonstrate the validity of the small-angle approximations. The most direct method is to truncate the McLaurin series for each of the trigonometric functions. Depending on the order of the approximation. Like we have approximated \[\cos \theta \approx 1 - \dfrac{{{\theta ^2}}}{2} \approx 1\].