Question

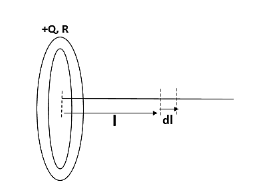
A non-conducting ring of radius $0.5m$carries a total charge of $1.11\times {{10}^{-10}}C$, distributed non-uniformly on its circumference, producing an electric field $\overrightarrow{E}$ everywhere in space. What is the value of the line integral $\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl$($l=0$ being the centre of the ring), in volts?
$\begin{align}
  & A.+2 \\
 & B.-1 \\
 & C.-2 \\
 & D.zero \\
\end{align}$

Answer 1

Hint: $\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl$ is a term which is equal to the potential. Therefore we can equate the potential at the given limits with this value of integral. This will give rise to the answer. Also remember the value of potential at infinity is considered to be zero. These all may help us to find out the answer for this question.

Complete answer:
First of all let us look at the integral given.
$\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl$ is the given integral which is generally equivalent to the formula for electric potential.
Therefore we can write that,
$\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl=V$
As the potential at a point is given by this particular formula, we can take the potential at the limit point and can find the difference.
That is,
${{V}_{i=0}}$, ${{V}_{i=\infty }}$
As we all know the electric potential at infinity is considered to be zero.
Therefore we can write that,
$\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl={{V}_{l=0}}$
Potential at the centre where the charge distribution is uniform or non-uniform is written as,
$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{R}$
Therefore we can write that,
$\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl={{V}_{l=0}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{R}$
Substituting the values in it will give,
$\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl=9\times {{10}^{9}}\dfrac{1.1\times {{10}^{-10}}}{0.5}V=2V$
Therefore the value of the integral given in the question is $\int_{l=\infty }^{0}{\overrightarrow{-E}\cdot }dl=2V$.

So, the correct answer is “Option A”.

Note:
Electric potential at the centre of a ring is equivalent to the potential due to a point charge. Whereas the electric field is found to be zero at the centre of the ring since the electric field at the half side of the ring will cancel out the other half. Electric potential is a scalar quantity also.