Question

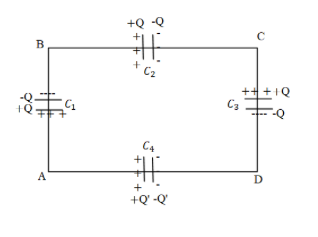
A network of four $10\mu F$ capacitors is connected to a 500V supply, as shown in fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the place with higher potential, equal and opposite to the charge on the plate with lower potential).

Answer 1

Hint:As there are three capacitors which are in series and there is one capacitor which behaves as parallel to the previous and therefore the equivalent capacitance can be calculated by taking all the three capacitor at once and applying the formula for the calculation of the equivalent capacitance and then apply the formula for the calculation of the equivalent capacitance for parallel capacitors.

Formula used:The formula of the charge on the capacitor is given by,
$Q = C \times V$
Where charge is given by Q the capacitance is C and the voltage difference is V.

Complete step by step answer:
It is given in the problem that a network with four$10\mu F$ capacitors is connected to a 500V supply and we need to find the equivalent capacitance and also we need to find the charge on each capacitor.

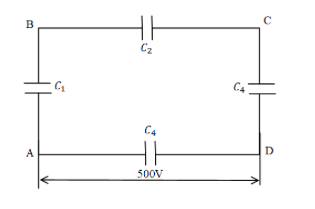
The equivalent capacitance for the three capacitors can be calculated as,
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Since,
$ \Rightarrow {C_1} = {C_2} = {C_3} = 10\mu F$
Therefore,
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}}$
$ \Rightarrow \dfrac{1}{{C'}} = \dfrac{3}{{10}}$
$ \Rightarrow C' = \dfrac{{10}}{3}\mu F$.
Now according to the diagram the three capacitors were parallel to the fourth capacitor which is also of equal capacitance.
${C_4} = 10\mu F$.
The equivalent capacitance is given by,
$ \Rightarrow {C_{eq.}} = C' + {C_4}$
$ \Rightarrow {C_{eq.}} = \dfrac{{10}}{3} + 10$
$ \Rightarrow {C_{eq.}} = \dfrac{{40}}{3}\mu F$
The equivalent capacitance of the capacitors is equal to${C_{eq.}} = \dfrac{{40}}{3}\mu F$.
Now let’s calculate the charge on each capacitor.
The formula of the charge on the capacitor is given by,
$Q = C \times V$
Where charge is given by Q the capacitance is C and the voltage difference is V.
Replace the values of capacitance and also the potential difference we get.
The charge on the capacitor ${C_4}$ is equal to,
$ \Rightarrow Q = C \times V$
$ \Rightarrow Q = 10 \times 500$
$ \Rightarrow Q = 5 \times {10^{ - 3}}C$.
The charge on the capacitors ${C_1},{C_2},{C_3}$ are equal to,
$ \Rightarrow Q = C' \times V$
Replace the value of capacitance ${C_1} = {C_2} = {C_3}$ and potential difference we get,
$ \Rightarrow Q = \dfrac{{10}}{3} \times 500$
$ \Rightarrow Q = \dfrac{5}{3} \times {10^{ - 3}}C$.
The equivalent capacitance is equal to ${C_{eq.}} = \dfrac{{40}}{3}\mu F$ and the charge on the capacitor ${C_1},{C_2},{C_3}$ and ${C_4}$ is equal to $Q = \dfrac{5}{3} \times {10^{ - 3}}C$ and $Q = 5 \times {10^{ - 3}}C$ respectively.

Note:The charge on all the capacitors is the same and equal to $10\mu F$ and the potential difference across the capacitors is equal to $500V$. The charge on the capacitors can be calculated by multiplying the potential difference with the net capacitance of the capacitor.