Question

A moving coil galvanometer allows a full scale current of${{10}^{-4}}A$. A series resistance of $2M\Omega $ is required to convert the above galvanometer into a voltmeter of range 0-5V. Therefore the value of shunt resistance required to convert the above galvanometer into an ammeter of range 0-10mA is:
A. $40\Omega $
B. $100\Omega $
C. $10\Omega $
D. $500\Omega $

Answer 1

Hint: You may recall that a galvanometer can be converted into voltmeter and ammeter by connecting a high and shunt resistance in series and parallel with the galvanometer respectively. Here, we have two cases. In the first case we have the conversion into voltmeter from which we could find the resistance of the galvanometer. This value can be used in the second case to find the shunt resistance used there.

Formula used:
Ohm’s law,
$V=I\left( R+G \right)$

Complete step-by-step answer:
In the question, we are given a galvanometer that shows full scale deflection when a current of${{10}^{-4}}A$passes through it. A series resistance of magnitude $2M\Omega $ is connected to the galvanometer so as to convert it into a voltmeter that has a range of 0-5V. We are supposed to find the value of shunt that is required to convert the galvanometer into voltmeter of range 0-10mA.

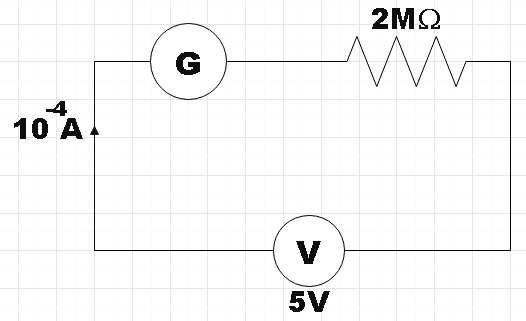
Let us recall that, for converting a galvanometer into voltmeter the shunt resistance is connected in series with the galvanometer. So the effective resistance in the circuit could be given by,
${{R}_{eff}}=G+S$
$\Rightarrow {{R}_{eff}}=\left( 2\times {{10}^{6}}+G \right)\Omega $
Now, on applying Ohm’s law we will get,
$V=I\left( R+G \right)$
$\Rightarrow 5={{10}^{-4}}\left( 2\times {{10}^{6}}+G \right)$
$\Rightarrow G=\left( 0.05-2 \right)\times {{10}^{6}}\Omega $
$\therefore G\Rightarrow -ve$
As the resistance of the given galvanometer cannot be a negative value, hence, the given condition is impossible.

Note: You shouldn’t try and by-heart the formulae for shunt resistance used for the conversion of galvanometer. All you have to remember is that the shunt is connected in parallel and series with the galvanometer to convert it into ammeter and voltmeter and then you could substitute the effective resistance in ohm's law and thus you could derive the formula from there.