Question

A motor boat going downstream crosses a float at a point $A$. $60$ minutes later it turns back and after some time it again crosses the float, now the float is at a distance of $12Km$ from the point $A$. The velocity of the stream is
A.$8km/h$
B.$4km/h$
C.$6km/h$
D.$10km/h$

Answer 1

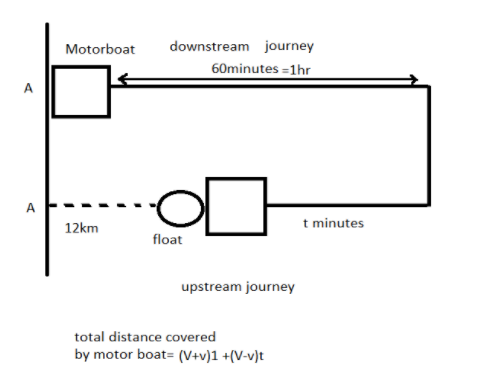
Hint: The question involves a simple concept of distance =speed$\times $time. Also, when moving downstream net speed of motor boat will be motor boat speed plus river flow speed.Let us assume that motor boat velocity be $V$, and river flow velocity be $v$.
Downward speed of boat with respect to ground =motor boat velocity+ velocity of river
$\Rightarrow V+v$
While on reverse journey of motor boat net speed of motor boat will be motor boat speed minus the river flow speed.
For reverse journey speed of boat will be
$V-v$
Also, float speed will be the same as river flow speed.
And net displacement of the motor boat will be $12km$ from point A.

Complete step by step answer:
Now to find the river flow velocity,let us assume that motor boat velocity be $V$, and river flow velocity be $v$.
The float is moving with the speed same as that of river flow that is $v$.
So the motor boat takes 60minutes=1hr to reach the end point of the journey.
Now let us suppose it takes $t\,hr$ time till it meets the float on its return journey
The float covers $12km$ in total time $\left( t+1 \right)hrs$ hrs,
Float speed=$v$,
The equation becomes,
$v\left( t+1 \right)=12.......\left( 1 \right)$
Downstream speed of motor boat=$\left( V+v \right)km/h$
Time for downstream journey=$60 minutes=1hr$
Reverse journey speed=$\left( V-v \right)km/h$
Time for reverse journey=$t\,hr$
Net displacement of motor boat from initial point=$12km$
So equation for motor boat is,
$\Rightarrow \left( V+v \right)1+\left[ -\left( V-v \right) \right]t=12km$
$\Rightarrow v\left( 1+t \right)+V-Vt=12$
Putting value from $\left( 1 \right)$
$\Rightarrow V-Vt=12-12$
$\Rightarrow t=\dfrac{V}{V}=1hr$
Putting this value in $\left( 1 \right)$,
$\Rightarrow v\left( 1+1 \right)=12km$
$\Rightarrow v=6km/h$

Hence the correct option for river flow speed is B.

Note:
Displacement and distance are two different quantities former is vector and latter is scalar.
Distance is the complete length of the path between any two points is called distance.
Displacement is the direct length between any two points when measured along the minimum path between them.