Question

A mill owner buys two types of machines A and B for his mill. Machines A occupies
1,000 sqm of area and requires 12 men to operate it; while machine B occupies 1,200 sqm of area and requires 8 men to operate it. The owner has 7,600 sqm of Area available and 72 men to operate the machines. If machine A produces 50 Units and machine B produces 40 units daily, how many machines of each type Should he buy to maximize the daily output? Use Linear Programming to find the solution.

Answer 1

Hint: In this type of problem we need to assume $ x{\text{ and y}} $ be the number of machines A,B respectively.
Then, we have to form an obtained equation in terms of $ x{\text{ and y}} $ and then plot them on a graph to get better understanding and finally check the condition which gives the maximum daily output.

Complete step-by-step answer:
Let's make a table to understand what is given and what we have to find?
 $
  {\text{ Machine A Machine B Maximum Available}} \\
  {\text{Area needed 1000sqm 1200sqm 7600sqm}} \\
  {\text{Labour force 12 8 72 }} \\
  {\text{Daily output 50 units 40 units -}} \\
    \\
  $
Let $ x{\text{ and y}} $ be the number of machines A and B respectively.
  Equation formed from area needed
 $
   \Rightarrow {\text{ 1000}}x + 1200y \leqslant {\text{ 7600 }} \\
   \Rightarrow {\text{ 5}}x + 6y \leqslant {\text{ 38 ------eq}}{\text{.1 }} \\
 $
Equation formed from labour force
 $
   \Rightarrow 12x + 8y \leqslant 72 \\
   \Rightarrow 3x + 2y \leqslant 18{\text{ -------eq}}{\text{.2}} \\
 $
And $
   \Rightarrow x \geqslant 0{\text{ ------eq}}{\text{.4}} \\
   \Rightarrow y \geqslant 0{\text{ -------eq}}{\text{.5}} \\
 $
Let Total output be $ z $
 $ \Rightarrow z = 50x + 40y{\text{ -------eq}}{\text{.6}} $
The problem is to maximize the daily output i.e. $ z $
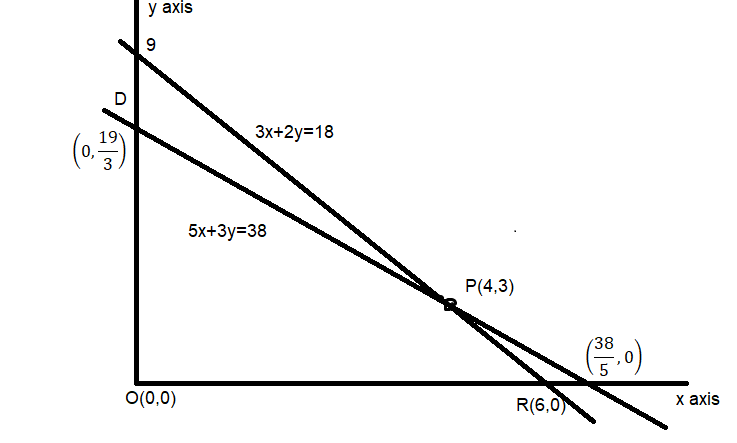
Now, for using Linear Programming we need to plot graph and for this we require the coordinates
From eq.4 and eq.5 , let O(0,0)
On putting y=0 in eq.2 we get $ x = 6 $ ,

let R(6,0)
Now, put $ x = 0 $ in eq.2 we get $ y = 9 $ .

Let S(0,9)
Now, put x=0 in eq.1, we get $ y = \dfrac{{19}}{3} $ .

Let $ {\text{D(0,}}\dfrac{{19}}{3}) $
Now find the intersection point of eq.1 and eq.2 we get $ {\text{P(4,3)}} $
Now plot all these coordinates on a graph. The vertices of the feasible region ORPD are O(0,0),R(6,0),P(4,3) and $ {\text{D(0,}}\dfrac{{19}}{3}) $
 $
  {\text{Point value of z = 50}}x + 40y \\
  {\text{at O(0,0), z = 0}} \\
  {\text{at R(6,0), z = 300}} \\
  {\text{at P(4,3), z = 320 }} \\
  {\text{at D(0,}}\dfrac{{19}}{3}){\text{z = }}\dfrac{{760}}{3} = 253.33 \\
    \\
 $
Thus we see that z is maximum at (4,3).
Hence, Number of machines A=4
And number of machines B=3.

Note: - Whenever you get this type of problem the key concept of solving is to make a table for understanding of given things in question. Then let the $ x,y $ for the commodity which is base of all other things given in the question like in this case number of machines A,B. And one more thing to be remember is that number of machines cannot be negative so $ x \geqslant 0{\text{ and y}} \geqslant {\text{0}} $ .