Question

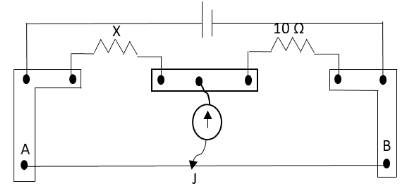
: A meter bridge is set-up as shown, to determine an unknown resistance X, using a standard 10 ohm resistor. The galvanometer shows null when tapping the key is a \[52\,{\text{cm}}\] mark. The end corrections are \[1\,{\text{cm}}\] and \[2\,{\text{cm}}\] for ends A and B. The determined value of X is:

A. \[10.2\,{\text{ohm}}\]
B. \[10.6\,{\text{ohm}}\]
C. \[10.8\,{\text{ohm}}\]
D. \[11.1\,{\text{ohm}}\]

Answer 1

Hint:Recall the process of using the meter bridge to determine the value of the unknown resistance using a known standard resistance. Use the balanced condition for the meter bridge. This condition gives the relation between the known resistance, unknown resistance and lengths of the two ends of the wire from the null point on the wire.

Formula used:
The balanced condition for the meter bridge to determine the unknown resistance using a standard resistance and galvanometer is given by
\[\dfrac{X}{R} = \dfrac{x}{{100 - x}}\] …… (1)
Here, \[X\] is the unknown resistance, \[R\] is the known standard resistance and \[x\] is the length of the null point from the one end of the wire.

Complete step by step answer:
We have given that the value of the known standard resistance is \[10\,{\text{ohm}}\].
\[R = 10\,{\text{ohm}}\]
The null point on the wire is obtained at the point J which is at a distance of \[52\,{\text{cm}}\] from the end A of the wire.
\[{\text{AJ}} = x = 52\,{\text{cm}}\]
The length of the wire used in the meter bridge to determine the unknown resistance is 100 cm.

Hence, the length of the wire from the end B of the wire is
\[{\text{JB}} = 100 - x = 100\,{\text{cm}} - 52\,{\text{cm}}\]
\[ \Rightarrow {\text{JB}} = 100 - x = 48\,{\text{cm}}\]
But we have given that the end corrections for the ends A and B are \[1\,{\text{cm}}\] and \[2\,{\text{cm}}\] respectively.
Hence, the lengths of the ends from the null point becomes
 \[{\text{AJ}} = x = 52\,{\text{cm}} + 1\,{\text{cm}}\]
\[ \Rightarrow {\text{AJ}} = x = 53\,{\text{cm}}\]
And
\[{\text{JB}} = 100 - x = 48\,{\text{cm}} + 2\,{\text{cm}}\]
\[ \Rightarrow {\text{JB}} = 100 - x = 50\,{\text{cm}}\]

Now use the balance condition for the meter bridge to determine the unknown resistance X.
Substitute \[10\,{\text{ohm}}\] for \[R\], \[53\,{\text{cm}}\] for \[x\] and \[50\,{\text{cm}}\] for \[100 - x\] in equation (1).
\[\dfrac{X}{{10\,{\text{ohm}}}} = \dfrac{{53\,{\text{cm}}}}{{50\,{\text{cm}}}}\]
\[ \Rightarrow X = \dfrac{{530}}{{50}}\]
\[ \therefore X = 10.6\,{\text{ohm}}\]
Therefore, the determined value of the unknown resistance is \[10.6\,{\text{ohm}}\].

Hence, the correct option is B.

Note: The students should keep in mind that the value of the determined resistance is more than 10 ohm. Hence, the distance of the null point 52 cm given is from the end A to have the value of the unknown resistance more than 10 ohm. If this distance is taken from point B then the determined value will be incorrect.