Question

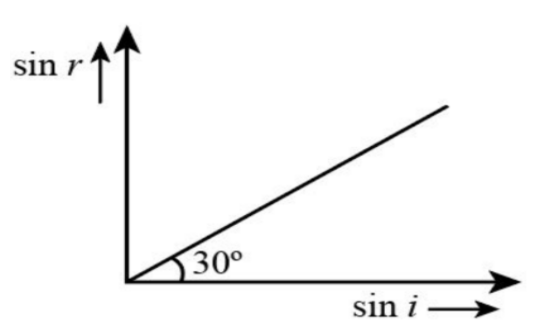
A medium shows relation between i and r as shown. If speed of light in the medium is nc then value of n is

(a) \[1.5\]
(b) \[2\]
(c) \[{2^{ - 1}}\]
(d) \[{3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}\]

Answer 1

Hint: From the concept of Brewster’s law of refraction, we can establish a relationship between the slope of the given graph and the polarising angle, which is equal to \[30^\circ \]. Also, we will use the concept of Snell’s law or the law of diffraction, which gives us the relationship between n and refractive index of the medium of light.

Complete step by step answer:
From the concept of Snell’s law of refraction, we can write:
\[n = \dfrac{1}{\mu }\]
Here \[\mu \] is the refractive index of the medium.
Refractive index can also be written as:
\[\begin{array}{l}
\dfrac{{\sin r}}{{\sin i}} = \dfrac{1}{\mu }\\
\Rightarrow \dfrac{{\sin i}}{{\sin r}} = \mu
\end{array}\]
Substitute \[\dfrac{1}{n}\] for \[\mu \] in the above expression.
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{1}{n}\]
We can also write the expression for the slope of the given graph from Brewster’s law.
\[\dfrac{{\sin r}}{{\sin i}} = S\]
Here, S represents the slope.
Rewriting the above expression, we get:
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{1}{S}\]
Substitute \[\dfrac{1}{n}\]for \[\dfrac{{\sin i}}{{\sin r}}\] in the above expression.
\[\begin{array}{l}
\dfrac{1}{n} = \dfrac{1}{S}\\
n = S
\end{array}\]……(1)
We can also write the value of slope from the given graph.
\[\begin{array}{c}
S = \tan 30^\circ \\
 = \dfrac{1}{{\sqrt 3 }}
\end{array}\]
Substitute \[\dfrac{1}{{\sqrt 3 }}\] for S in equation (1).
\[n = \dfrac{1}{{\sqrt 3 }}\]
Rewrite the above expression to check which option is correct.
\[n = {3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}\]
Therefore, if the speed of light is nc, then the value of n is equal to \[{3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}\]

So, the correct answer is “Option D”.

Note:
 While writing the slope of the given graph, do not forget to take the inverse of it so that the relationship between slope S and n can be established as a result of which value of n can be determined. Also, do not forget to rewrite the fractional value of n into its simplest form to get the correct answer.