Question

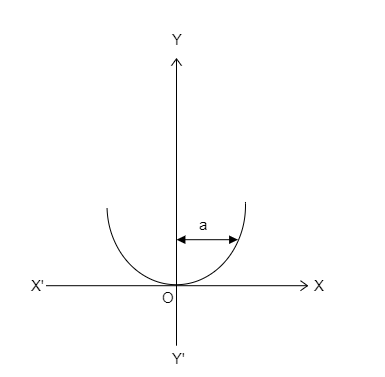
A mass $m$is fixed at $x = a$ on a parabolic wire with its axis vertical and vertex at the origin as shown in the figure. The equation of the parabola is ${x^2} = 4ay$ . The wireframe is rotating at a constant angular velocity $\omega $ about Y-axis. Find the acceleration of the bead.

A. $\dfrac{a}{4}{\omega ^2}$
B. $a{\omega ^2}$
C. Zero
D. $\dfrac{{{\omega ^2}}}{a}$

Answer 1

Hint:-Here it is mentioned that the wire rotates at a constant angular velocity. As the mass is placed on this rotating wireframe, it is safe to say that the bead of some mass will execute uniform circular motion about the vertical axis. So the acceleration of the bead will be the centripetal acceleration of circular motion.

Formulas used:
The centripetal acceleration of a body is given by, ${a_c} = \dfrac{{{v^2}}}{r}$ where $v$ is the linear velocity of the body and $r$ is the radius of the circle described by the rotating body.
The linear velocity of a rotating body can be expressed as $v = r\omega $ where $\omega $ is the angular velocity of the body and $r$ is the radius of the circle described by the rotating body.


Complete step-by-step solution:-
Step 1: Sketch a figure depicting the rotation of the bead and list the parameters known from the question.

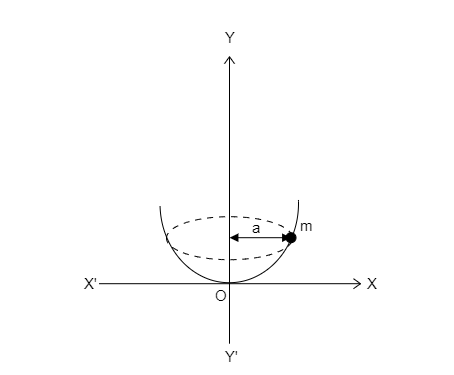
The above figure shows the rotation of the bead.
It is mentioned that the bead is placed on the wire which has a shape of a parabola. The equation of the parabola is given to be ${x^2} = 4ay$ . This implies that the parabola exists in the positive half of the y-axis.
The bead is placed at a position $x = a$ on the parabola as seen in the above figure. The bead describes a circle and the radius of the circle will be equal to the distance from the vertical axis i.e., $r = a$ .
The mass of the bead is given to be $m$ and the angular velocity of the wireframe as it rotates is given to be $\omega $ .
Step 2: Express the centripetal acceleration of the bead.
The centripetal acceleration of the bead can be expressed as ${a_c} = \dfrac{{{v^2}}}{r}$ -------- (1)
where $v$ is the linear velocity of the bead and $r$ is the radius of the circle described by the rotating bead.
Since the linear velocity of the bead can be expressed in terms of its angular velocity as $v = r\omega $equation (1) becomes ${a_c} = \dfrac{{{{\left( {r\omega } \right)}^2}}}{r} = {\omega ^2}r$
So the centripetal acceleration of the bead is given by, ${a_c} = {\omega ^2}r$ --------- (2)
Substituting for $r = a$ in equation (2) we get, ${a_c} = {\omega ^2}a$ .
So we have the acceleration of the bead as ${\omega ^2}a$ .
Thus the correct option is B.

Note:- Here the rotating bead is placed on the rotating wireframe. So the angular velocity of the bead will be the same as that of the rotating wireframe. The magnitude of the centripetal acceleration will be constant as both $\omega $ and $a$ are constant. However, its direction changes at every point of the circle described by the bead so that it always points towards the centre. So we cannot say that the centripetal acceleration is a constant vector.