Question

A marketing firm that, of 200 households surveyed, 80 used neither brand A nor brand B soap, 60 used only brand A soap and for every household that used both brands of soap, 3 used only brand B soap. How many of the 200 households surveyed used both brands of soap.

Answer 1

Hint: To solve this problem, we will consider A as the set containing number of households using brand A and B as the set containing number of households using brand B. Now, we will use the formula that $n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right)$. Here, $A\bigcup B$ determines the set containing all the elements of A and B, while $A\bigcap B$ determines the set having only the common elements of A and B. Along with this, we will also make use of $A'\bigcap B'=(A\bigcup B)'$.

Complete step-by-step answer:
Let us now consider the given question,

Since it is given that 80 households use neither Brand A nor Brand B, then we have that $A'\bigcap B'$ = 80 (here, $A'$ means all the events excluding that in set A and $B'$ means all the events excluding set B). Now, we use the following theorem that $A'\bigcap B'=(A\bigcup B)'$ (where ‘ stands for complement of an event as shown for the case of $A'$ and $B'$ ). Thus, we have, $(A\bigcup B)'=80$.
(Thus, $n\left( A\bigcup B \right)=200-80=120$).
It is also given that 60 households use only brand A and that three times as many households use Brand B exclusively as use both brands.
If x is the number of households that use both Brand A and Brand B, then 3x use Brand B alone (as per the information given in the problem).
Thus, we have, $n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right)$. By substituting, we have,
$120=\left( 60+x \right)+\left( 3x+x \right)-x$
[n(A) means the entire set containing elements of A. Thus, we have to add x to A to get n(A). Similar is the case with n(B)]
Solving the above equation we get,
$120=60+4x$
Let us subtract 60 from both sides to get,
$4x=60$
Hence, x=15

So, 15 people use both brand A and brand B of soaps.

Therefore, the final answer is option (a).


Note: To avoid the algebraic expressions in set, one of the easier ways to solve is to represent the above problem on the Venn diagram. One can easily calculate the value of x using the space of $n(A\bigcap B)$ in the Venn diagram.
We have shown in the above solution that:
60 households use only brand A means:
$n\left( A \right)-n\left( A\bigcap B \right)=60$
x is the number of households that use both Brand A and Brand B which means:
$n\left( A\bigcap B \right)=x$
3x use Brand B alone which means:
$n\left( B \right)-n\left( A\bigcap B \right)=3x$
Representing the above information on the Venn diagram we get,

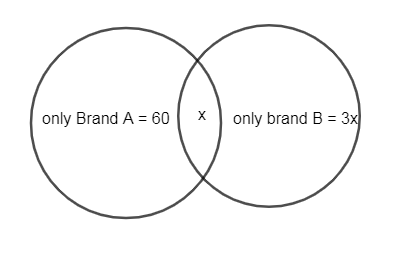
From the above Venn diagram,
 $n\left( A\bigcup B \right)=60+x+3x$
We have calculated in the above solution that $n\left( A\bigcup B \right)=120$ so substituting this value in the above equation we get,
$\begin{align}
  & 120=60+x+3x \\
 & \Rightarrow 60=4x \\
\end{align}$
Dividing 4 on both the sides of the equation we get,
$15=x$
Hence, we have got the number of households who use both brands A and B is 15.