
A manufacturer makes two products A and B. Product A sells at Rs. 200 each and takes $\dfrac{1}{2}$hour to make. Product B sells at Rs. 300 each and takes one hour to make. There is a permanent order for 14 numbers of product A and 16 numbers of product B. A working week consists of 60 hours of production and the weekly turnover must not be less than Rs. 10,000. If the profit on each of product A is Rs 20 and product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also, find the profit.
Answer
576.6k+ views
Hint: To solve this question, we need to use the Linear Programming Approach. First, we need to create a table which will help us form the inequalities according to the conditions mentioned in the question. Then, you need to convert those inequalities to equations and plot those equations in the graph. Next step, includes finding the common region in the graph with the help of the inequations. Choose all the corner points in the graph and then use those points to substitute in the maximization equation and find the maximum profit along with the number of units to manufacture for product A and B. The highest value is your profit and $x$, $y$ will be your decision variables.
Complete step by step answer:
Let us first make a table for product A and product B. Before that, let us consider $x$ units manufactured of product A and $y$ units manufactured of product B.
Number of units cannot be negative; therefore, we can say that $x,y\ge 0$.
Also, the working hours per week consists of 60 hours of production and the weekly revenue is to be Rs. 10000.
The number of units at least to be made of product A is 14 and product B is 16.
Therefore, the constraints are
Selling price constraint,
\[\begin{align}
& 200x+300y\ge 10,000 \\
& 2x+3y\ge 100
\end{align}\]
Time constraint,
$\dfrac{1}{2}x+1\times y\le 60$
$\begin{align}
& \dfrac{x}{2}+y\le 60 \\
& \dfrac{x+2y}{2}\le 60 \\
& x+2y\le 120
\end{align}$
Number of units constraint,
$x\ge 14$, $y\ge 16$
The next part of the question emphasizes on the profit made on product A and product B. Product A makes a profit of Rs. 20 and product B makes a profit of Rs. 30.
Therefore, Maximum profit (Z) = $20x+30y$
Thus, the mathematical formulation of the given linear programming problem is
Maximize Z = $20x+30y$............ (1)
subject to
\[2x+3y\ge 100\]
$x+2y\le 120$
$x\ge 14$, $y\ge 16$,$x,y\ge 0$
The next step is to convert the inequalities to equations, we get
$2x+3y=100$
$x+2y=120$
$x=14$, $y=16$, $x=0$, $y=0$
Now, let us draw the equations in the graph and find the required value.
In order to plot the line, $2x+3y=100$
Let us consider $x=0$, therefore, $2\left( 0 \right)+3y=100$
$\begin{align}
& 0+3y=100 \\
& y=\dfrac{100}{3}
\end{align}$
Therefore, point A$\left( 0,\,\dfrac{100}{3} \right)$.
Let us now consider $y=0$, therefore, $2x+3\left( 0 \right)=100$
$2x+0=100$
$\begin{align}
& x=\dfrac{100}{2} \\
& =50
\end{align}$
Therefore, point B $\left( 50,\,0 \right)$.
We got the points A and B for the line equation $2x+3y=100$.
Similarly, let us find out for the line equation, $x+2y=120$
Let us first consider $x=0$, therefore, $0+2y=120$
$\begin{align}
& 2y=120 \\
& y=\dfrac{120}{2} \\
& =60
\end{align}$
Therefore, point C $\left( 0,\,60 \right)$.
Let us consider $y=0$, therefore, $x+2\left( 0 \right)=120$
$\begin{align}
& x+0=120 \\
& =120
\end{align}$
Therefore, point D $\left( 120,\,0 \right)$
We got points C and D for the line equation \[x+2y=120\].
$x=14$ line will be parallel to $y-$axis and $y=16$ line will be parallel to $x-$axis.
$x,y\ge 0$ indicates that the answer is lying in the first quadrant. Let us plot the obtained points and equations of line and create a graph.
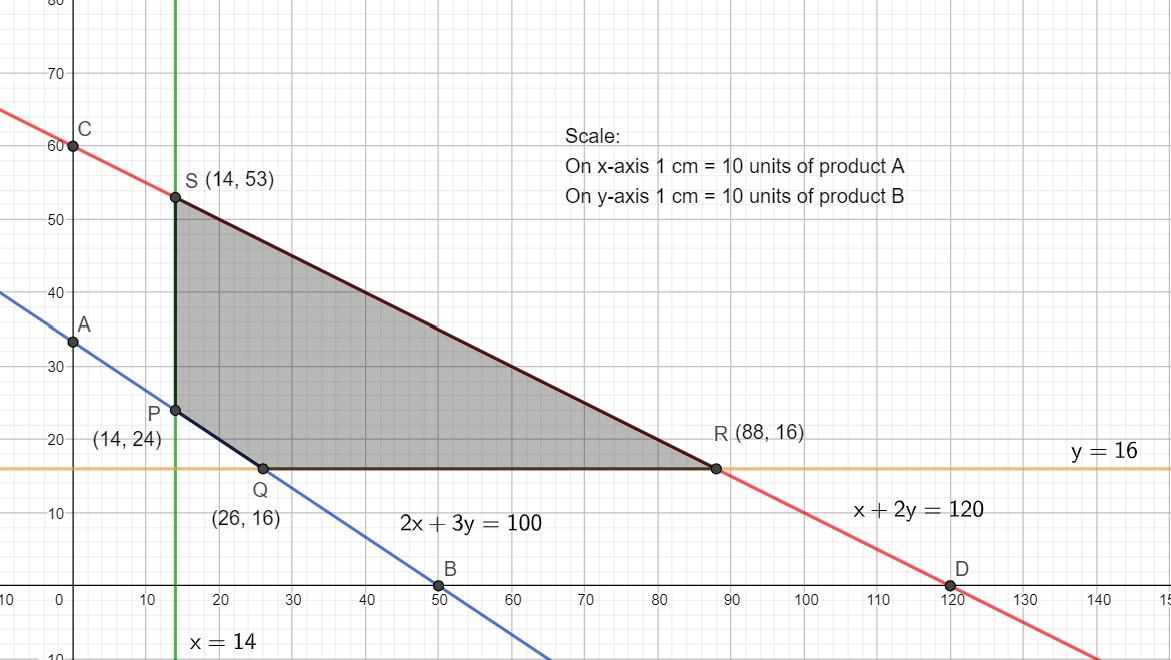
There are two parts on either side of the line, one part is the part towards the origin and the other part is the part farther from the origin.
According to the constraints,
\[2x+3y\ge 100\], indicates the green line and it is greater than equal, which indicates that the value of this inequation is farther from the origin or above the line.
$x+2y\le 120$, indicates the blue line and it is less than equal, which indicates that the value of the inequation is towards the origin or below the line.
$x\ge 14$, indicates the red line and it is greater than equal, which indicates that the value of the inequation is away from the origin or on the right part of the line.
$y\ge 16$, indicates the origin line and it is greater than equal, which indicates that the value of the inequation is away from the origin or on the top part of the line.
Therefore, the shaded region is the common solution for all the inequation which is also the area of polygon PQRS,
Now, let us write down the corner points of polygon PQRS, because out of all these four corner points one point will give us the maximum profit value.
P (14, 24); Q (26, 16); R (88, 16); S (14, 53)
Let us substitute each point $\left( x,y \right)$ in equation (1), we get the maximum profit value
Z = $20x+30y$
P (14, 24): Z = 20 (14) + 30 (24)
= 280 + 720
= 1000
Q (26, 16): Z = 20 (26) + 30 (16)
= 520 + 480
= 1000
R (88, 16): Z = 20 (88) + 30 (16)
= 2240
S (14, 53): Z = 20 (14) + 30 (53)
= 280 + 1590
= 1870
Out of all the values, the maximum value is R (88, 16) = $\left( x,y \right)$.
Hence, to get maximum profit, 88 units of product A need to be manufactured and 16 units of product B need to be manufactured. The maximum profit is Rs. 2240/-.
Note: In this question, we need to figure out if this is the maximization problem or the minimization problem, according to the question mentioned. Here, profit should always be maximum hence the given question is a maximization type problem.
Complete step by step answer:
Let us first make a table for product A and product B. Before that, let us consider $x$ units manufactured of product A and $y$ units manufactured of product B.
Number of units cannot be negative; therefore, we can say that $x,y\ge 0$.
| Selling price (Rs.) | Manufacturing Time (hrs.) | |
| Product A ($x$) | 200 | $\dfrac{1}{2}$ |
| Product B ($y$) | 300 | 1 |
Also, the working hours per week consists of 60 hours of production and the weekly revenue is to be Rs. 10000.
The number of units at least to be made of product A is 14 and product B is 16.
Therefore, the constraints are
Selling price constraint,
\[\begin{align}
& 200x+300y\ge 10,000 \\
& 2x+3y\ge 100
\end{align}\]
Time constraint,
$\dfrac{1}{2}x+1\times y\le 60$
$\begin{align}
& \dfrac{x}{2}+y\le 60 \\
& \dfrac{x+2y}{2}\le 60 \\
& x+2y\le 120
\end{align}$
Number of units constraint,
$x\ge 14$, $y\ge 16$
The next part of the question emphasizes on the profit made on product A and product B. Product A makes a profit of Rs. 20 and product B makes a profit of Rs. 30.
Therefore, Maximum profit (Z) = $20x+30y$
Thus, the mathematical formulation of the given linear programming problem is
Maximize Z = $20x+30y$............ (1)
subject to
\[2x+3y\ge 100\]
$x+2y\le 120$
$x\ge 14$, $y\ge 16$,$x,y\ge 0$
The next step is to convert the inequalities to equations, we get
$2x+3y=100$
$x+2y=120$
$x=14$, $y=16$, $x=0$, $y=0$
Now, let us draw the equations in the graph and find the required value.
In order to plot the line, $2x+3y=100$
Let us consider $x=0$, therefore, $2\left( 0 \right)+3y=100$
$\begin{align}
& 0+3y=100 \\
& y=\dfrac{100}{3}
\end{align}$
Therefore, point A$\left( 0,\,\dfrac{100}{3} \right)$.
Let us now consider $y=0$, therefore, $2x+3\left( 0 \right)=100$
$2x+0=100$
$\begin{align}
& x=\dfrac{100}{2} \\
& =50
\end{align}$
Therefore, point B $\left( 50,\,0 \right)$.
We got the points A and B for the line equation $2x+3y=100$.
Similarly, let us find out for the line equation, $x+2y=120$
Let us first consider $x=0$, therefore, $0+2y=120$
$\begin{align}
& 2y=120 \\
& y=\dfrac{120}{2} \\
& =60
\end{align}$
Therefore, point C $\left( 0,\,60 \right)$.
Let us consider $y=0$, therefore, $x+2\left( 0 \right)=120$
$\begin{align}
& x+0=120 \\
& =120
\end{align}$
Therefore, point D $\left( 120,\,0 \right)$
We got points C and D for the line equation \[x+2y=120\].
$x=14$ line will be parallel to $y-$axis and $y=16$ line will be parallel to $x-$axis.
$x,y\ge 0$ indicates that the answer is lying in the first quadrant. Let us plot the obtained points and equations of line and create a graph.

There are two parts on either side of the line, one part is the part towards the origin and the other part is the part farther from the origin.
According to the constraints,
\[2x+3y\ge 100\], indicates the green line and it is greater than equal, which indicates that the value of this inequation is farther from the origin or above the line.
$x+2y\le 120$, indicates the blue line and it is less than equal, which indicates that the value of the inequation is towards the origin or below the line.
$x\ge 14$, indicates the red line and it is greater than equal, which indicates that the value of the inequation is away from the origin or on the right part of the line.
$y\ge 16$, indicates the origin line and it is greater than equal, which indicates that the value of the inequation is away from the origin or on the top part of the line.
Therefore, the shaded region is the common solution for all the inequation which is also the area of polygon PQRS,
Now, let us write down the corner points of polygon PQRS, because out of all these four corner points one point will give us the maximum profit value.
P (14, 24); Q (26, 16); R (88, 16); S (14, 53)
Let us substitute each point $\left( x,y \right)$ in equation (1), we get the maximum profit value
Z = $20x+30y$
P (14, 24): Z = 20 (14) + 30 (24)
= 280 + 720
= 1000
Q (26, 16): Z = 20 (26) + 30 (16)
= 520 + 480
= 1000
R (88, 16): Z = 20 (88) + 30 (16)
= 2240
S (14, 53): Z = 20 (14) + 30 (53)
= 280 + 1590
= 1870
Out of all the values, the maximum value is R (88, 16) = $\left( x,y \right)$.
Hence, to get maximum profit, 88 units of product A need to be manufactured and 16 units of product B need to be manufactured. The maximum profit is Rs. 2240/-.
Note: In this question, we need to figure out if this is the maximization problem or the minimization problem, according to the question mentioned. Here, profit should always be maximum hence the given question is a maximization type problem.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Which prominent US inventor was known as the Wizard class 12 social science CBSE

Which state in India is known as the Granary of India class 12 social science CBSE

Draw a ray diagram of compound microscope when the class 12 physics CBSE

When was the first election held in India a 194748 class 12 sst CBSE

How is democracy better than other forms of government class 12 social science CBSE




