Question

A man weighs $80\,kg$. He stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of $5\,m{s^{ - 2}}$. What would be the reading on the scale?
(A) $1200$
(B) $500$
(C) $0$
(D) $144$

Answer 1

Hint: According to Newton’s third law of motion, when the lift moves upwards, then the force of the man inside the lift will act downwards. The reading on the scale shows the reading which is equal to the sum of the force of man due to the acceleration of the lift and the force due to gravity.

Formulae Used:
The reading on the scale is equal to the sum of the force due to gravity and the force due to the acceleration of the lift
$R = {F_g} + {F_a}$
Where, $R$ is the reading in the scale, ${F_g}$ force due to gravity and ${F_a}$ is the force due to acceleration of lift.

Complete step-by-step solution:
Given that,
Man weight, $m = 80\,kg$
Acceleration of lift, $a = 5\,m{s^{ - 2}}$

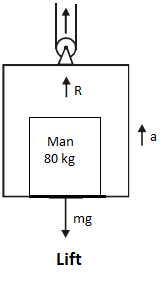
The reading in the weight scale is,
$R = {F_g} + {F_a}\,...............\left( 1 \right)$
By substituting the force formula in the above equation, then the above equation is written as,
$R = mg + ma\,...............\left( 2 \right)$
Where, $m$ is the mass of the man, $g$ is the acceleration due to gravity and $a$ is the acceleration of the lift.
By taking the mass values as common in the equation (2), then the above equation is written as,
$R = m\left( {g + a} \right)$
By substituting the mass value, acceleration due to gravity and the acceleration of the lift in the above equation, then
$R = 80\left( {10 + 5} \right)$
Here, the acceleration due to gravity is taken as $10\,m{s^{ - 2}}$ for easy calculation,
Then by adding the above equation,
$R = 80 \times 15$
On multiplying the above equation, then
$R = 1200\,N$
Thus, the above equation shows the reading which shows in the reading scale.
Hence, the option (A) is correct.

Note:- The force due to gravity and the force due to acceleration of the lift, both the forces are acting downwards, so both are added. So, when the body is moving upward in lift with some acceleration, the weight of the body is greater than the actual weight of the body, when the weight of the body is measured in that lift.