Question

A man walks $4km$ due west, $500m$ due south finally $750m$ in south west direction. The distance and magnitude of displacement travelled by the man are:
A. $4646.01m\,\,and\,\,5250m$
B. $5250m\,\,and\,\,4646.01m$
C. $4550.01m\,\,and\,\,2300m$
D. None of the above

Answer 1

Hint:You can easily solve this question by firstly, drawing a diagram about how the man walks and where he reaches at the end. Also, know the difference between distance and displacement, distance is the scalar sum of his walks, while displacement is the vector sum of his walks.

Complete step-by-step solution:
We will try to solve the question exactly like we told in the hint section of the solution to the question. This will be pretty easy once we draw the diagram of the man’s walks, so, here is the diagram that we have drawn:

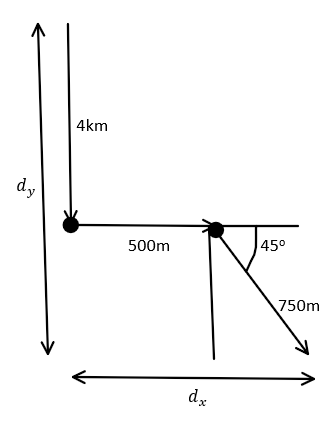
We can see that the man firstly walks due west, then due south and then, finally, due south-west.
First, let us find the distance he covered:
We know that distance is simply the scalar sum of the distances that he travelled in parts. To find the total distance travelled, all we need to do is a simple scalar sum of all his walks. Let us do that now:
Distance $\, = \,4000m + 500m + 750m$
Distance $ = \,5250m$
Now, we need to find the displacement of the man from the point he started.
For this, we have already drawn ${d_x}$ and ${d_y}$ in the diagram. The vector sum of ${d_x},\,{d_y}$ is the final displacement of the man from the point where he started.
Let us calculate ${d_x},{\kern 1pt} {d_y}$ first.
For ${d_x}$, we have:
${d_x}\, = \,500m\, + \,750\cos 45^\circ $
Simplifying this, we get:
${d_x}\, = \,893.99\,m$
Similarly, for ${d_y}$, we can easily see that:
${d_y}\, = \,4000m + 750\sin 45^\circ $
Simplifying, we get:
${d_y}\, = \,4393.99$
To find the total displacement, we now simply have to do their vector sum:
Displacement $\, = \,\sqrt {{{\left( {893.99} \right)}^2} + {{\left( {4393.99} \right)}^2}} $
Displacement $\, = \,4646.01m$
Now that we have both the values of distance and displacement, we can confidently say that option (B) is the correct option.

Note:- You can also solve this question by firstly, doing the vector sum of his walk due west and south, and then do the vector sum of their resultant and his walk due south-west. That method will not only be longer, but calculation heavy as well and there will be room for you to commit mistakes. This method that we depicted is probably the fastest and the simplest one.