Question

A man walks $20\,m$at an angle of ${60^ \circ }$ east of north. How far north has he travelled?

Answer 1

Hint: To solve this question we should think about resolving it into components. We saw in the discussion of vector addition that a group of vectors can be combined to form a single vector (the resultant). A single vector can be decomposed into a variety of vectors, which when added together yield the original vector. Components of the original vector are vectors that add up to the original vector. Resolving into components is the method of splitting a vector into its constituents.

Complete step by step answer:
Let us understand the distance and displacement a little much. The term "distance" refers to "how much ground an object has travelled" during its motion. Displacement is a vector quantity that describes "how far an object is out of place", it is the object's total shift in location.

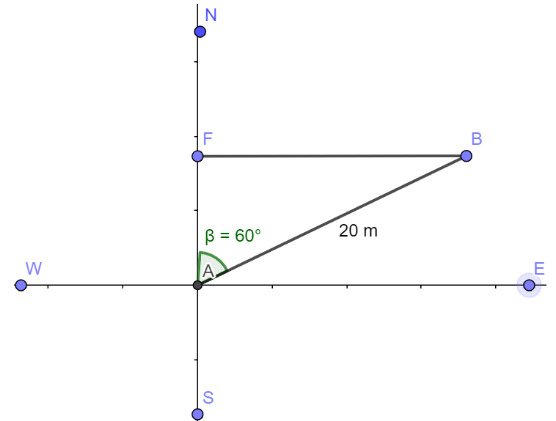
If we resolve the AB line there will be two component:
One in the direction of North ${Y_{north}} = 20 \times \cos {60^ \circ }$
Another in the direction of East ${X_{east}} = 20 \times \sin {60^ \circ }$
So, the component of the distance in the north direction is given as:
${Y_{north}} = 20 \times \cos {60^ \circ }$
$\Rightarrow {Y_{north}} = 20 \times \left( {\dfrac{1}{2}} \right)$
$\therefore {Y_{north}} = 10\,\,m$

Hence, he travelled 10 m in the north direction.

Note:To solve this kind of question we should keep some point in our mind. Most importantly the resolving of vector components. Components are the sections of a two-dimensional vector. The components of a vector reflect the vector's effect in a given direction. The combined influence of the two components is equal to the single two-dimensional vector's influence