Question

A man stands 9m away from a flag – pole. He observes that the angle of elevation of the top of the pole is ${{28}^{\circ }}$ and the depression of the bottom of the pole is ${{13}^{\circ }}$ . Calculate the height of the pole.

Answer 1

Hint: To find the height of the pole first we need to draw the diagram to understand the data in question. Take AB as a pole where $AB=AE+BE$ then find BE with the help of $\tan {{13}^{\circ }}$ and AE with the help of $\tan {{28}^{\circ }}$ . We can use the value of $\tan {{13}^{\circ }}=0.23086$ and $\tan {{28}^{\circ }}=0.5317.$

Complete step-by-step answer:

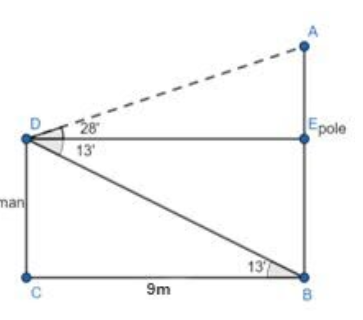
A man stands 9m away from a flag pole i.e. $BC=DE=9m$ .
He observes that the angle of elevation of the top of the pole is ${{28}^{\circ }}$ i.e. $\angle ADE={{28}^{\circ }}$ and the angle of depression of the bottom of the pole is ${{13}^{\circ }}$ i.e. $\angle EDB={{13}^{\circ }}$ .
$CD=BE.$
In $\Delta BDE$ .
$\tan \theta =\dfrac{\text{BE}}{DE}$ .
$\tan {{13}^{\circ }}=\dfrac{BE}{9}$ ( Here $DE=9cm$) .
$0.23086=\dfrac{\text{BE}}{\text{9}}$ ( Here $\tan {{13}^{\circ }}=0.23086$).
Now, multiply both side by $'9'$ we get –
$\begin{align}
  & 0.23056\times 9=BE \\
 & 2.077=BE. \\
\end{align}$
In $\Delta ADE$
$\tan \theta =\dfrac{\text{AE}}{\text{DE}}$ .
$\tan {{28}^{\circ }}=\dfrac{\text{AE}}{\text{9}}$ ( where $DE=9m$ ).
$0.53.17=\dfrac{AE}{\text{9}}$ ( HERE $\tan \theta =0.5317$ ).
Multiplying both side by $'9'$ we get –
$\begin{align}
  & 0.5317\times 9=AE \\
 & 4.785=AE \\
\end{align}$
Height of the pole $=AE+BE$
$=4.785+2.077$
$=6.862m.$
Hence the height of the pole is $6.862m.$

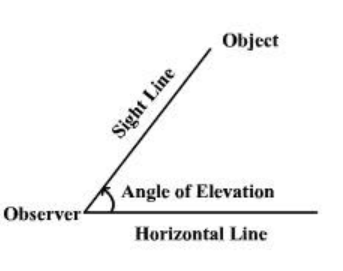
Note: In this question students may get confused because of angle of elevation and angle of depression. They should know the difference between angle of elevation and angle of depression. The term angle of elevation denotes the angle between the horizontal upward to an object.

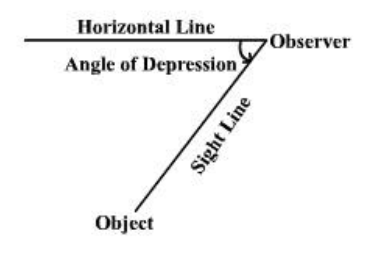
The term of depression denotes the angle from the horizontal down was to an object.

The angle of elevation and the angle of depression are congruent.