
A man standing on the deck of a ship, which is 10m above the water level. He observes the angle of elevation of the top of a lighthouse as $60^\circ $ and the angle of depression of the base of the lighthouse as $30^\circ $. Find the height of the light house.
A) $40m$
B) $50m$
C) $60m$
D) $30m$

Answer
585.9k+ views
Hint: In any right-angled triangle, for any angle:
\[
The{\text{ }}sine{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(a){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\
The{\text{ }}cosine{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side\;}}{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }} \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(b){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\; \\
The{\text{ }}tangent{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\;\;\;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{\;\;the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}\;\;\;\;\;\;\; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(c){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\
\]
Complete step-by-step answer:
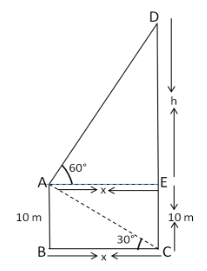
Let CD be the lighthouse and suppose the man is standing on the deck of a ship at point A.
The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. So, the angle of depression of the base C of the lighthouse CD observed from A is $30^\circ $
The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. So, the angle of elevation of the top D of the lighthouse CD observed from A is $60^\circ $
So, $\angle EAD = 60^\circ $and $\angle BCA = 30^\circ $
In $\vartriangle AED$,using property (c ) from the hint:-
$
\Rightarrow \tan 60^\circ = \dfrac{{DE}}{{AE}} = \dfrac{h}{x} \\
\Rightarrow h = x\tan 60^\circ \\
\Rightarrow h = \sqrt 3 x \ldots \ldots \ldots \ldots \ldots \ldots (1) \\
$
In $\vartriangle ABC$,using property (c ) from the hint:-
$
\Rightarrow \tan 30^\circ = \dfrac{{AB}}{{BC}} = \dfrac{{10}}{x} \\
\Rightarrow 10 = x\tan 30^\circ \\
\Rightarrow x = 10\sqrt 3 \ldots \ldots \ldots \ldots \ldots \ldots (2) \\
$
Now substitute the value of x from equation (2) to equation (1):
$
\Rightarrow h = \sqrt 3 x \\
\Rightarrow h = \sqrt 3 (10\sqrt 3 ) \\
\Rightarrow h = 10\sqrt 3 (\sqrt 3 ) \\
\Rightarrow h = 10(3) \\
\Rightarrow h = 30m \\
$
So, option (D) is the correct answer.
Note: If you are only looking to estimate a distance, then you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller.
Please remember the values of these to solve such kinds of questions.
\[
The{\text{ }}sine{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(a){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\
The{\text{ }}cosine{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side\;}}{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }} \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(b){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\; \\
The{\text{ }}tangent{\text{ }}of{\text{ }}the{\text{ }}angle{\text{ }} = \;\;\;\;\;\;\dfrac{{the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{\;\;the{\text{ }}length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}\;\;\;\;\;\;\; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \; \ldots \;(c){\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\
\]
Complete step-by-step answer:
Let CD be the lighthouse and suppose the man is standing on the deck of a ship at point A.
The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. So, the angle of depression of the base C of the lighthouse CD observed from A is $30^\circ $
The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. So, the angle of elevation of the top D of the lighthouse CD observed from A is $60^\circ $
So, $\angle EAD = 60^\circ $and $\angle BCA = 30^\circ $
In $\vartriangle AED$,using property (c ) from the hint:-
$
\Rightarrow \tan 60^\circ = \dfrac{{DE}}{{AE}} = \dfrac{h}{x} \\
\Rightarrow h = x\tan 60^\circ \\
\Rightarrow h = \sqrt 3 x \ldots \ldots \ldots \ldots \ldots \ldots (1) \\
$
In $\vartriangle ABC$,using property (c ) from the hint:-
$
\Rightarrow \tan 30^\circ = \dfrac{{AB}}{{BC}} = \dfrac{{10}}{x} \\
\Rightarrow 10 = x\tan 30^\circ \\
\Rightarrow x = 10\sqrt 3 \ldots \ldots \ldots \ldots \ldots \ldots (2) \\
$
Now substitute the value of x from equation (2) to equation (1):
$
\Rightarrow h = \sqrt 3 x \\
\Rightarrow h = \sqrt 3 (10\sqrt 3 ) \\
\Rightarrow h = 10\sqrt 3 (\sqrt 3 ) \\
\Rightarrow h = 10(3) \\
\Rightarrow h = 30m \\
$
So, option (D) is the correct answer.
Note: If you are only looking to estimate a distance, then you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller.
Please remember the values of these to solve such kinds of questions.
| Angle in Degrees | Sin | Cos | Tan |
| $0^\circ $ | 0 | 1 | 0 |
| $30^\circ $ | $\dfrac{1}{2}$ | $\dfrac{{\sqrt 3 }}{2}$ | $\dfrac{1}{{\sqrt 3 }}$ |
| $45^\circ $ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{1}{{\sqrt 2 }}$ | 1 |
| $60^\circ $ | $\dfrac{{\sqrt 3 }}{2}$ | $\dfrac{1}{2}$ | $\sqrt 3 $ |
| $90^\circ $ | 1 | 0 | $\infty $ |
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




