Question

A man standing on a railway platform noticed that a train took 21 seconds to cross the platform (this means the time elapsed from the moment the engine enters the platform till the last compartment leaves the platform) which is 88 meters long, and that it took 9 seconds to pass him. Assuming that the train was moving with uniform speed, what is the length of the train in meters?
\[\begin{align}
  & A.5 \\
 & B.60 \\
 & C.66 \\
 & D.72 \\
\end{align}\]

Answer 1

Hint: In this question, we are given time taken by train to cross platform, length of platform and time taken by train to pass a man. We have to find the length of the train. For this, we will first draw a small diagram to understand the concept properly. After that, we will use distance time formula to calculate required length. The formula that we will use is given as $\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$.

Complete step by step answer:
Let us first draw a diagram to understand the question carefully. Here, we are supposing the length of the train to be l.

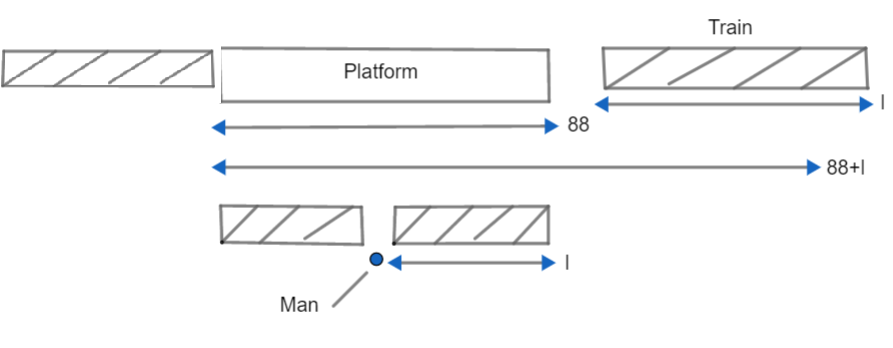
Here we are given that, man notices that the train took 21 seconds to cross the platform, so it must have covered the distance of platform and length of train in 21 seconds. As we have supposed the length of the train to be l meters. Therefore, the total distance covered in 21 seconds will be (88+l)m. Now let us suppose the speed of train v meters per second. Therefore, distance covered in 21 seconds will also be given by $\text{Distance}=\text{speed}\times \text{time}$ that is
$\text{Distance}=\left( 21v \right)m$.
Both distance found are same, therefore
\[21v=88+l\cdots \cdots \cdots \cdots \left( 1 \right)\]
Now we are given that, train crosses man in 9 seconds. Since man can be considered as a point only, therefore, a train crosses a point in 9 second and hence, distance covered by train will be its length. Hence, distance covered by train in 9 seconds will be l. Also v is the speed of the train. So, distance can also be given as $\text{Distance}=\text{speed}\times \text{time}$ that is
$\text{Distance}=\left( 9v \right)m$
Therefore, \[9v=l\cdots \cdots \cdots \cdots \left( 2 \right)\]
From (2), we can have $v=\dfrac{l}{9}$ putting it in (1), we get:
\[\begin{align}
  & 21\left( \dfrac{l}{9} \right)=88+l \\
 & \Rightarrow \dfrac{7}{3}l=88+l \\
 & \Rightarrow \dfrac{7}{3}l-l=88 \\
\end{align}\]
Taking LCM of 3 on left side of the equation, we get:
\[\begin{align}
  & \Rightarrow \dfrac{7l-3l}{3l}=88 \\
 & \Rightarrow \dfrac{4l}{3}=88 \\
\end{align}\]
Dividing both sides by $\dfrac{3}{4}$ we get:
\[\begin{align}
  & \Rightarrow l=88\times \dfrac{3}{4} \\
 & \Rightarrow l=22\times 3 \\
 & \Rightarrow l=66 \\
\end{align}\]
Therefore, the length of the train is 66m.

So, the correct answer is “Option C”.

Note: Students should note that this question can be tricky when considering the length of train to be the total distance covered in 21 seconds. Don't forget to consider man as a point and use the information for finding distance covered by train to be equal to length of train. Students can make mistakes in taking distance equal to speed or time. For example in (1), they can make the mistake of taking 21 to be equal to 88+l rather than 21v.