Question

A man running on a horizontal road at $8km{{h}^{-1}}$ finds the rain falling vertically. He increases his speed to$12km{{h}^{-1}}$ and finds that the drops make angle $30{}^\circ $ with the vertical. Find the speed and direction of the rain with respect to the road.
A. $4kmph,{{\tan }^{-1}}\left( 2 \right)$ with the vertical
B. $4kmph,{{\tan }^{-1}}\left( \dfrac{1}{2} \right)$ with the vertical
C. $8kmph,{{\tan }^{-1}}\left( \dfrac{3}{2} \right)$ with the vertical
D. $4\sqrt{7}kmph,{{\tan }^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)$ with the vertical

Answer 1

Hint: From the first case where the man’s velocity is$8km{{h}^{-1}}$, we could find the horizontal component of the velocity of the rain. Then from the second part, you could find the vertical component too. The magnitude of these two will give the velocity of rain with respect to the road. Simple trigonometry will give the angle made with the vertical.

Complete answer:
In the question, we are given a man who is running on a horizontal road at a speed of $8km{{h}^{-1}}$ finds the rain to be falling vertically and when this man increases his speed to $12km{{h}^{-1}}$finds that the rain make $30{}^\circ $ with the vertical. We are asked to find the speed and direction of the rain with respect to the road.
As the man moving at $8km{{h}^{-1}}$ finds the rain to be falling vertically, we could say that velocity of rain with respect to man in the horizontal direction is zero, that is,
${{\left( {{V}_{rm}} \right)}_{x}}=0$
$\Rightarrow {{\left( {{V}_{r}}-{{V}_{m}} \right)}_{x}}=0$
${{\left( {{V}_{r}} \right)}_{x}}={{V}_{m}}=8km{{h}^{-1}}$ ……………………………………………. (1)
Now when the man increased his pace to $12km{{h}^{-1}}$ he found the rain to be falling at an angle$30{}^\circ $, so now, the velocity of rain with respect to man along the x-direction is not zero, so,
${{V}_{x}}'={{\left( {{V}_{rm}} \right)}_{x}}\ne 0$
$\Rightarrow {{V}_{x}}'={{\left( {{V}_{r}}-{{V}_{m}} \right)}_{x}}$
$\Rightarrow {{V}_{x}}'={{\left( 8-12 \right)}_{x}}$
$\therefore {{V}_{x}}'=-4km{{h}^{-1}}$ ………………………………………………………….. (2)
Now the situation could be represented as,

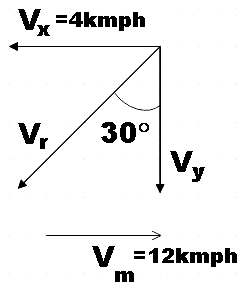
From the figure,
$\tan 30{}^\circ =\dfrac{{{V}_{x}}}{{{V}_{y}}}$
$\Rightarrow {{V}_{y}}=\dfrac{{{V}_{x}}}{\tan 30{}^\circ }$
$\therefore {{V}_{y}}=4\sqrt{3}km{{h}^{-1}}$ …………………………………………. (3)
We are asked to find the speed and direction of the rain with respect to the road.

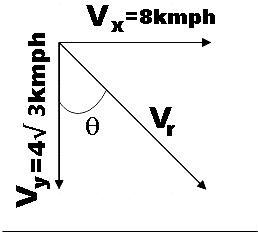
Let, ${{V}_{r}}$ be the velocity of rain with respect to the road. We have its vertical and horizontal components from (1) and (3), so,
${{V}_{r}}=\sqrt{{{V}_{x}}^{2}+{{V}_{y}}^{2}}$
$\Rightarrow {{V}_{r}}=\sqrt{{{8}^{2}}+{{\left( 4\sqrt{3} \right)}^{2}}}$
$\Rightarrow {{V}_{r}}=\sqrt{64+48}=\sqrt{112}$
$\therefore {{V}_{r}}=4\sqrt{7}km{{h}^{-1}}$
Now for the angle $\theta $,
$\tan \theta =\dfrac{8}{4\sqrt{3}}$
$\Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{8}{4\sqrt{3}} \right)$
$\therefore \theta ={{\tan }^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)$
Therefore, we found that, the speed and direction of the rain with respect to the road are $4\sqrt{7}kmph,{{\tan }^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)$ with the vertical respectively.

Hence, option D is found to be the correct answer.

Note:
We should be careful while dealing with problems related to relative motion of bodies. We should never forget to specify with respect to what the mentioned velocity is. Now, always remember to use a diagram to represent the velocities and related components for better clarity. Also, one should be careful about the direction.