Question

A man rides his motorcycle at the speed of 50km/hr. He has to spend Rs. 2 per Km on petrol. If it rides it at a faster speed of 80km/hr. The petrol cost increases to Rs. 3 per Km. He has at most Rs. 120 to spend on petrol and he has one hour time. Determine the maximum distance that the man can travel.

Answer 1

Hint: In this particular question first find the equation which we have to maximize and the constraints according to given conditions in the problem then solve them by using graphical method by plotting all the constraints so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Let the man ride x hours with the speed of 50 Km/hr. and y hours with the speed of 80 Km/hr.
So the distance covered by the man in x hours with speed of 50 Km/hr. = 50x Km.
And the distance covered by the man in y hours with speed of 80 Km/hr. = 80y Km.
So the equation which we have to maximize is, Z = 50x + 80y
Now it is given that he has a maximum of 1 hour.
Therefore there is constraint of $x + y \leqslant 1$
Now it is given that when he goes with a speed of 50 km/hr. he has to spend Rs. 2 per Km.
So the total money spend in x hours = $2 \times 50x = 100x$
Now it is also given that when he goes with a speed of 80 km/hr. he has to spend Rs. 3 per Km.
So the total money spend in y hours = $3 \times 80y = 240y$
Now it is given that he has a maximum 120 Rs.
So there is an another constraint that, $100x + 240y \leqslant 120$
We can simplify this constraint by dividing by 20 throughout we have,
$ \Rightarrow 5x + 12y \leqslant 6$
And we all know that x and y cannot be negative so, $x \geqslant 0,y \geqslant 0$
So the problem statement is that we have to maximize
Z = 50x + 80y
Subject to constraints
$x + y \leqslant 1$
$5x + 12y \leqslant 6$
$x \geqslant 0,y \geqslant 0$
Now we solve this by using a graphical method.
Now plot these lines on a graph.
So, $x + y \leqslant 1$
Now calculate x and y axis coordinates so that we can plot this easily.
So for x coordinate substitute y = 0 we have,
$ \Rightarrow x + 0 \leqslant 1$
$ \Rightarrow x \leqslant 1$
So point on x-axis is (1, 0)
Now for y coordinate substitute x = 0 we have,
$ \Rightarrow 0 + y \leqslant 1$
$ \Rightarrow y \leqslant 1$
So point on y-axis is (0, 1)
So join these points as shown in the above figure.
Now plot $5x + 12y \leqslant 6$
Now calculate x and y axis coordinates so that we can plot this easily.
So for x coordinate substitute y = 0 we have,
$ \Rightarrow 5x + 0 \leqslant 6$
$ \Rightarrow x \leqslant \dfrac{6}{5}$
So point on x-axis is ($\dfrac{6}{5}$, 0)
Now for y coordinate substitute x = 0 we have,
$ \Rightarrow 0 + 12y \leqslant 6$
$ \Rightarrow y \leqslant \dfrac{1}{2}$
So point on y-axis is (0, $\dfrac{1}{2}$)
So join these points as shown in the figure.
Now, x $ \geqslant $0, and y $ \geqslant $ 0 are the regions positive side of y-axis and positive side of x-axis respectively as shown in the graph.
Now the common region is marked with yellow color.

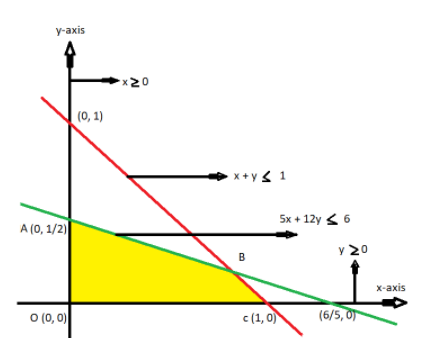
So ABCOA is the common region of these lines.
Now find the coordinates of point B.
As point B is the intersection of lines x + y = 1 and 5x + 12y = 6
So multiply by 5 in first equation and subtract from second we have,
$ \Rightarrow 5x + 5y - \left( {5x + 12y} \right) = 5 - 6$
$ \Rightarrow - 7y = - 1$
$ \Rightarrow y = \dfrac{1}{7}$
Now put this value in any above equation so we have,
$ \Rightarrow x + \dfrac{1}{7} = 1$
$ \Rightarrow x = 1 - \dfrac{1}{7} = \dfrac{6}{7}$
So the coordinates of point B is, $\left( {\dfrac{6}{7},\dfrac{1}{7}} \right)$.
Now find out the value of Z at these points we have,
At point A (0, 1/2)
$ \Rightarrow Z = 50x + 80y = 50\left( 0 \right) + 80\left( {\dfrac{1}{2}} \right) = 40$
At point B $\left( {\dfrac{6}{7},\dfrac{1}{7}} \right)$
$ \Rightarrow Z = 50x + 80y = 50\left( {\dfrac{6}{7}} \right) + 80\left( {\dfrac{1}{7}} \right) = \dfrac{{300 + 80}}{7} = \dfrac{{380}}{7} = 54.28$
At point C (1, 0)
$ \Rightarrow Z = 50x + 80y = 50\left( 1 \right) + 80\left( 0 \right) = 50$
At point O (0, 0)
$ \Rightarrow Z = 50x + 80y = 50\left( 0 \right) + 80\left( 0 \right) = 0$
So as we see that the maximum value of Z is at point B $\left( {\dfrac{6}{7},\dfrac{1}{7}} \right)$ and the maximum value of Z is 54.28 Km.
So the maximum distance a man can cover is 54.28 Km.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that to maximize the function graphically first we have to find out the common region of the given equations than mark all boundary points as above we marked then evaluate the value of z at all these points as above calculated then check at which point Z is maximized, so at this particular point the value of z is the required answer.