Question

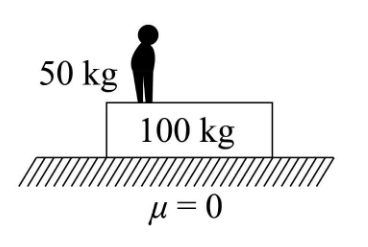
A man of mass $ 50kg $ is standing on a $ 100kg $ plank kept on a frictionless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed $ 6\dfrac{m}{s} $ towards right relative to the plank, then amount of muscle energy spent by the man is

Answer 1

Hint : To solve this question, we will be using the conservation laws for the given system and also we will have to consider the frame of reference of the man with respect to the plank as well as the frictionless surface.
(A) Conservation of angular momentum
 $ {{M}_{1}}{{V}_{1}}={{M}_{2}}{{V}_{2}} $
Where $ {{M}_{1}} $ and $ {{M}_{2}} $ are the masses. $ {{V}_{1}} $ and $ {{V}_{2}} $ are the velocities .
(B) Formula for kinetic energy
 $ K=\dfrac{1}{2}M{{V}^{2}} $
Where $ M $ is the mass and $ V $ is the velocity.

Complete Step By Step Answer:
Now for the first thing, we will be focusing on the data given.
Given, the mass of the man $ {{M}_{1}}=50kg $
And the mass of the plank $ {{M}_{2}}=100kg $
The frictional coefficient $ \mu =0 $
The velocity of the man with respect to the plank $ {{V}_{1}}=6\dfrac{m}{s} $
The velocity of the plank with respect to the frictionless floor is $ {{V}_{2}} $
Whereas, the velocity of the man with respect to the frictionless floor $ V=6\dfrac{m}{s}-{{V}_{2}} $
Now, according to the data given to us, there is no external force acting on the system and therefore, the total momentum of the system is conserved. Hence, using the formulae for conservation of momentum
 $ {{M}_{1}}V={{M}_{2}}{{V}_{2}} $
 $ \Rightarrow 50(6-{{V}_{2}})=100{{V}_{2}} $
 $ \begin{align}
  & \Rightarrow 300-50{{V}_{2}}=100{{V}_{2}} \\
 & \Rightarrow 150{{V}_{2}}=300 \\
 & \Rightarrow {{V}_{2}}=\dfrac{300}{150} \\
\end{align} $
 $ \Rightarrow {{V}_{2}}=2\dfrac{m}{s} $
Therefore, the velocity of the plank with respect to the frictionless surface is $ {{V}_{2}}=2\dfrac{m}{s} $ which is in the opposite direction to that of the velocity of the man. Because the floor is frictionless, when the man starts moving on the plank, the plank starts moving in the opposite direction.
Now, if we look at the figure closely, we will notice that the muscle energy which is spent by the man is equal to the total kinetic energy of the man and the plank system together.
We use the formula for kinetic energy as
 $ \begin{align}
  & K=\dfrac{1}{2}{{M}_{1}}{{V}^{2}}+\dfrac{1}{2}{{M}_{2}}{{V}^{2}} \\
 & \Rightarrow K=\dfrac{1}{2}(50){{(6-2)}^{2}}+\dfrac{1}{2}(100){{(2)}^{2}} \\
 & \Rightarrow K=600kg\cdot \dfrac{{{m}^{2}}}{{{s}^{2}}}\times (\dfrac{N}{kg\cdot \dfrac{m}{{{s}^{2}}}}) \\
 & \Rightarrow K=600J \\
\end{align} $
Finally, we can say that the energy used by the muscles of the man is equal to $ 600J $ .

Note :
Keep in mind to see the frame of reference while writing the relative velocities of man and plank with the frictionless floor. Also, remember that the velocity of the plan with respect to the man is in the opposite direction to that of the velocity of the man.