Question

A man is walking towards a vertical pillar in a straight path, at a uniform speed. At a certain point $A$ on the path, he observes that the angle of elevation of the top of the pillar is ${30^ \circ }$. After walking for $10\min $ from $A$ in the same direction, at a point $B$, he observes that the angle of elevation of the top of the pillar is ${60^ \circ }$. Then the time taken (in minutes) by him, from $B$ to reach the pillar is:
A) $6$
B) $10$
C) $20$
D) $5$

Answer 1

Hint: Let the height of the vertical pillar be $h$. At $A$, its angle of elevation is ${30^ \circ }$. Then at $B$, angle of elevation becomes ${60^ \circ }$. So if it travels ${x_1}$ distance from $A$ to $B$, then speed$ = \dfrac{{{x_1}}}{{10}}$. With some speed he travels from $B$ to pillar. Now you can find the answer.

Complete step-by-step answer:
According to the question, here a man is walking towards a vertical pillar.
Let $PQ$ be the vertical pillar.

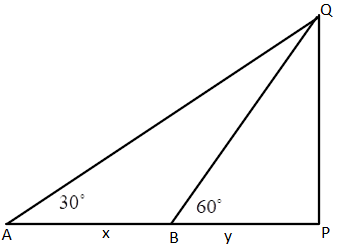
Let the height of the vertical pillar $PQ$ be $h$.
And man is moving towards the pillar. Let the speed of man be $v$.
So at $A$, it is given that the angle of elevation of the top of the pillar is ${30^ \circ }$.
That means, $\angle PAQ = {30^ \circ }$
Then again he moves for $10\min $ and reaches point $B$. Let him travel $x$ distance on reaching point $A$ to $B$. That is, $AB = x$.
At point $B$ angle of elevation changes to ${60^ \circ }$which means $\angle PBQ = {60^ \circ }$.
Let's assume the distance of point $B$ from pillar be $y$. So, $BP = y$.
As we know that man moves $A$ to $B$ in $10\min $, so,
speed$ = v = \dfrac{{AB}}{{10}}$$ = \dfrac{x}{{10}}mper\min $.
Now, in $\vartriangle APQ$
$\tan A = \dfrac{{perpendicular}}{{base}}$
$\tan {30^ \circ } = \dfrac{{PQ}}{{AP}} = \dfrac{h}{{x + y}}$
We know $\angle PAQ = {30^ \circ }$ and $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
So,
$
  \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + y}} \\
  h = \dfrac{{x + y}}{{\sqrt 3 }} \\
 $ (1)
Now in $\vartriangle BPQ$
$\angle PBQ = {60^ \circ }$
$\tan {60^ \circ } = \dfrac{{PQ}}{{BP}}$
$\sqrt 3 = \dfrac{h}{y}$
So we get,
$h = \sqrt 3 y$ (2)
Now equating equation (1) and (2)
$
  \sqrt 3 y = \dfrac{{x + y}}{{\sqrt 3 }} \\
  3y = x + y \\
    \\
 $
$\dfrac{y}{x} = \dfrac{1}{2}$ (3)
As speed$ = \dfrac{x}{{10}}$
So from some point $B$ to pillar, it will move with some speed
So, speed$ = \dfrac{{distance}}{{time}}$
Let time taken to reach pillar from $B$ be $t$.
$v = \dfrac{y}{t}$
We know , $v = \dfrac{x}{{10}}$
So,
$
  \dfrac{x}{{10}} = \dfrac{y}{t} \\
  t = \dfrac{y}{x} \times 10 = \dfrac{1}{2} \times 10 \\
  t = 5\min \\
 $

So option D is correct.

Note: Angle of elevation is the upward angle from the horizontal line to the line of sight from observer to some point of interest. But if that angle goes downward, it is called the angle of depression.