
When a man is standing, raindrops appear to him falling at $60^\circ $ from the horizontal from his front side. When he is travelling at a speed of $5{\text{km}}{{\text{h}}^{ - 1}}$ on a horizontal road, they appear to him falling at $30^\circ $ from the horizontal from his front side. Find the actual speed of the rain (in ${\text{km}}{{\text{h}}^{ - 1}}$ ).
A) 3
B) 4
C) 5
D) 6
Answer
585.6k+ views
Hint: The man can be considered as the frame of reference for the falling raindrops. So it is the relative velocity of rain to the man that makes the different angles with the horizontal. The actual speed of the rain refers to the velocity of rain with respect to the ground. It will be the sum of the relative velocity of rain to the man and the velocity of the man.
Formula used:
The actual velocity of the motion of an object in a moving frame of reference is given by, ${\vec v_o} = {\vec v_{o/fr}} + {\vec v_{fr}}$ where ${\vec v_{o/fr}}$ is the velocity of the object with respect to the frame of reference and ${\vec v_{fr}}$ is the velocity of the frame of reference.
The magnitude of velocity $\vec v = {\vec v_x}\hat i + {\vec v_y}\hat j$ is given by, $v = \sqrt {{v_x}^2 + {v_y}^2} $ where ${v_x}$ and ${v_y}$ are the components of the velocity in the x-direction and y-direction respectively.
Complete step by step answer:
Step 1: Sketch a rough diagram describing the velocities of the man and rain when the man is stationary and when he is moving. And obtain an expression for the actual velocity of rain by resolving into its components.
We consider two cases.
Case 1: The man is at rest and the raindrops make an angle of $60^\circ $ with the horizontal as they fall. The figure given below depicts the velocity of rain relative to the man resolved into its components.
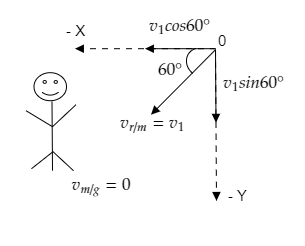
Since the man is at rest, his velocity relative to the ground is zero, i.e., ${v_{m/g}} = 0$ .
The velocity of rain relative to the man ${v_{r/m}} = {v_1}$ is resolved into its x-component $\Rightarrow {v_x} = - {v_1}\cos 60^\circ = - \dfrac{{{v_1}}}{2}$ and y-component ${v_y} = - {v_1}\sin 60^\circ = - \dfrac{{\sqrt 3 {v_1}}}{2}$ .
So, the velocity of rain relative to the man can be expressed as
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
Then the actual velocity of rain i.e., the velocity of rain relative to the ground is given by, ${\vec v_{r/g}} = {\vec v_{r/m}} + {\vec v_{m/g}}$ ------- (1)
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$ and ${\vec v_{m/g}} = 0\hat i + 0\hat j$ in equation (1) we get,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
i.e., the velocity of rain is given by,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$ ----------- (2)
Case 2: The man is moving with some velocity along the horizontal direction and the raindrops make an angle of $30^\circ $ as they fall. The figure given below depicts the velocity of rain relative to the man resolved into its components.

The man moves with a velocity ${v_{m/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$ on a horizontal road. So this velocity only has x-component i.e., ${\vec v_{m/g}} = 5\hat i$ .
As the man is moving, the velocity of rain relative to the man changes and becomes ${v_{r/m}} = {v_2}$. This is resolved into its x-component ${v_x} = - {v_2}\cos 30^\circ = - \dfrac{{\sqrt 3 {v_2}}}{2}$ and y-component ${v_y} = - {v_2}\sin 30^\circ = - \dfrac{{{v_2}}}{2}$ .
So, the velocity of rain relative to the man can be expressed as
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j$
$\Rightarrow {v_{r/m}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j$ and ${\vec v_{m/g}} = 5\hat i$ in equation (1) we get,
$\Rightarrow {v_{r/g}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j + 5\hat i = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
i.e., the velocity of rain is given by,
$\Rightarrow {v_{r/g}} = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$ ----------- (3)
Step 2: Equate equations (2) and (3) to find the values of ${v_1}$ and ${v_2}$ .
Equation (2) gives
${\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
and equation (3) gives ${v_{r/g}} = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
On equating equations (2) and (3) we get,
$\Rightarrow - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
We can equate the coefficients of $\hat i$ and $\hat j$ on the R.H.S and L.H.S of the above equation.
On equating coefficients of $\hat i$ we get,
$\Rightarrow - \dfrac{{{v_1}}}{2} = 5 - \dfrac{{\sqrt 3 {v_2}}}{2}$ -------- (4)
And on equating coefficients of $\hat j$ we get,
$\Rightarrow - \dfrac{{\sqrt 3 {v_1}}}{2} = - \dfrac{{{v_2}}}{2}$ -------- (5)
From equation (5) we obtain ${v_2} = \sqrt 3 {v_1}$ and
On substituting this value in equation (4) we get,
$\Rightarrow - \dfrac{{{v_1}}}{2} = 5 - \left( {\dfrac{{\sqrt 3 \times \sqrt 3 {v_1}}}{2}} \right)$
On simplifying, the above equation becomes
$\Rightarrow \dfrac{{3{v_1}}}{2} - \dfrac{{{v_1}}}{2} = 5$ and finally we have,
$\Rightarrow {v_1} = 5$ and ${v_2} = \sqrt 3 {v_1} = 5\sqrt 3 $
Step 3: Back substitute the value of ${v_1}$ in equation (2) to find the actual velocity of the rain.
Substituting ${v_1} = 5$ in equation (2) we get,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{5}{2}\hat i - \dfrac{{5\sqrt 3 }}{2}\hat j$
Then the magnitude of the velocity of rain will be
$\Rightarrow {v_{r/g}} = \sqrt {{{\left( { - \dfrac{5}{2}} \right)}^2} + {{\left( { - \dfrac{{5\sqrt 3 }}{2}} \right)}^2}} = \sqrt {\dfrac{{25}}{4} + \dfrac{{75}}{4}} $
The value is obtained to be
$\Rightarrow {v_{r/g}} = \sqrt {\dfrac{{100}}{4}} = \sqrt {25} = 5{\text{km}}{{\text{h}}^{ - 1}}$
$\therefore $ The actual speed of the rain is ${v_{r/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$. Hence, the correct option is C.
Note:
Alternate method:
When the man is at rest i.e., ${v_{m/g}} = 0$ , the actual velocity of the rain given by equation (1) is ${\vec v_{r/g}} = {v_x}\hat i + {v_y}\hat j$ where ${v_x}$ and ${v_y}$ are the components of the velocity in the x-direction and y-direction respectively.
Since the angle made by the velocity of the raindrops with the horizontal is $60^\circ $ ,$\tan 60^\circ = \dfrac{{{v_y}}}{{{v_x}}} = \sqrt 3 $
$ \Rightarrow {v_y} = \sqrt 3 {v_x}$ ----------- (A)
When the man moves with a velocity of ${v_{m/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$ in the horizontal direction, the actual velocity of the rain given by equation (1) is ${\vec v_{r/g}} = \left( {5 + {v_x}} \right)\hat i + {v_y}\hat j$
Here, the angle made by the velocity of the raindrops with the horizontal is $30^\circ $.
So, $\tan 30^\circ = \dfrac{{{v_y}}}{{5 + {v_x}}} = \dfrac{1}{{\sqrt 3 }}$
$ \Rightarrow \sqrt 3 {v_y} = 5 + {v_x}$ ------------ (B)
From equations (A) and (B) we get, $3{v_x} = 5 + {v_x}$ or ${v_x} = \dfrac{5}{2}$
And then ${v_y} = \dfrac{{5\sqrt 3 }}{2}$
So the resultant velocity will be ${v_{r/g}} = \sqrt {{{\left( {\dfrac{5}{2}} \right)}^2} + {{\left( {\dfrac{{5\sqrt 3 }}{2}} \right)}^2}} = 5{\text{km}}{{\text{h}}^{ - 1}}$
Formula used:
The actual velocity of the motion of an object in a moving frame of reference is given by, ${\vec v_o} = {\vec v_{o/fr}} + {\vec v_{fr}}$ where ${\vec v_{o/fr}}$ is the velocity of the object with respect to the frame of reference and ${\vec v_{fr}}$ is the velocity of the frame of reference.
The magnitude of velocity $\vec v = {\vec v_x}\hat i + {\vec v_y}\hat j$ is given by, $v = \sqrt {{v_x}^2 + {v_y}^2} $ where ${v_x}$ and ${v_y}$ are the components of the velocity in the x-direction and y-direction respectively.
Complete step by step answer:
Step 1: Sketch a rough diagram describing the velocities of the man and rain when the man is stationary and when he is moving. And obtain an expression for the actual velocity of rain by resolving into its components.
We consider two cases.
Case 1: The man is at rest and the raindrops make an angle of $60^\circ $ with the horizontal as they fall. The figure given below depicts the velocity of rain relative to the man resolved into its components.

Since the man is at rest, his velocity relative to the ground is zero, i.e., ${v_{m/g}} = 0$ .
The velocity of rain relative to the man ${v_{r/m}} = {v_1}$ is resolved into its x-component $\Rightarrow {v_x} = - {v_1}\cos 60^\circ = - \dfrac{{{v_1}}}{2}$ and y-component ${v_y} = - {v_1}\sin 60^\circ = - \dfrac{{\sqrt 3 {v_1}}}{2}$ .
So, the velocity of rain relative to the man can be expressed as
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
Then the actual velocity of rain i.e., the velocity of rain relative to the ground is given by, ${\vec v_{r/g}} = {\vec v_{r/m}} + {\vec v_{m/g}}$ ------- (1)
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$ and ${\vec v_{m/g}} = 0\hat i + 0\hat j$ in equation (1) we get,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
i.e., the velocity of rain is given by,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$ ----------- (2)
Case 2: The man is moving with some velocity along the horizontal direction and the raindrops make an angle of $30^\circ $ as they fall. The figure given below depicts the velocity of rain relative to the man resolved into its components.

The man moves with a velocity ${v_{m/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$ on a horizontal road. So this velocity only has x-component i.e., ${\vec v_{m/g}} = 5\hat i$ .
As the man is moving, the velocity of rain relative to the man changes and becomes ${v_{r/m}} = {v_2}$. This is resolved into its x-component ${v_x} = - {v_2}\cos 30^\circ = - \dfrac{{\sqrt 3 {v_2}}}{2}$ and y-component ${v_y} = - {v_2}\sin 30^\circ = - \dfrac{{{v_2}}}{2}$ .
So, the velocity of rain relative to the man can be expressed as
$\Rightarrow {\vec v_{r/m}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j$
$\Rightarrow {v_{r/m}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j$ and ${\vec v_{m/g}} = 5\hat i$ in equation (1) we get,
$\Rightarrow {v_{r/g}} = - \dfrac{{\sqrt 3 {v_2}}}{2}\hat i - \dfrac{{{v_2}}}{2}\hat j + 5\hat i = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
i.e., the velocity of rain is given by,
$\Rightarrow {v_{r/g}} = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$ ----------- (3)
Step 2: Equate equations (2) and (3) to find the values of ${v_1}$ and ${v_2}$ .
Equation (2) gives
${\vec v_{r/g}} = - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j$
and equation (3) gives ${v_{r/g}} = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
On equating equations (2) and (3) we get,
$\Rightarrow - \dfrac{{{v_1}}}{2}\hat i - \dfrac{{\sqrt 3 {v_1}}}{2}\hat j = \left( {5 - \dfrac{{\sqrt 3 {v_2}}}{2}} \right)\hat i - \dfrac{{{v_2}}}{2}\hat j$
We can equate the coefficients of $\hat i$ and $\hat j$ on the R.H.S and L.H.S of the above equation.
On equating coefficients of $\hat i$ we get,
$\Rightarrow - \dfrac{{{v_1}}}{2} = 5 - \dfrac{{\sqrt 3 {v_2}}}{2}$ -------- (4)
And on equating coefficients of $\hat j$ we get,
$\Rightarrow - \dfrac{{\sqrt 3 {v_1}}}{2} = - \dfrac{{{v_2}}}{2}$ -------- (5)
From equation (5) we obtain ${v_2} = \sqrt 3 {v_1}$ and
On substituting this value in equation (4) we get,
$\Rightarrow - \dfrac{{{v_1}}}{2} = 5 - \left( {\dfrac{{\sqrt 3 \times \sqrt 3 {v_1}}}{2}} \right)$
On simplifying, the above equation becomes
$\Rightarrow \dfrac{{3{v_1}}}{2} - \dfrac{{{v_1}}}{2} = 5$ and finally we have,
$\Rightarrow {v_1} = 5$ and ${v_2} = \sqrt 3 {v_1} = 5\sqrt 3 $
Step 3: Back substitute the value of ${v_1}$ in equation (2) to find the actual velocity of the rain.
Substituting ${v_1} = 5$ in equation (2) we get,
$\Rightarrow {\vec v_{r/g}} = - \dfrac{5}{2}\hat i - \dfrac{{5\sqrt 3 }}{2}\hat j$
Then the magnitude of the velocity of rain will be
$\Rightarrow {v_{r/g}} = \sqrt {{{\left( { - \dfrac{5}{2}} \right)}^2} + {{\left( { - \dfrac{{5\sqrt 3 }}{2}} \right)}^2}} = \sqrt {\dfrac{{25}}{4} + \dfrac{{75}}{4}} $
The value is obtained to be
$\Rightarrow {v_{r/g}} = \sqrt {\dfrac{{100}}{4}} = \sqrt {25} = 5{\text{km}}{{\text{h}}^{ - 1}}$
$\therefore $ The actual speed of the rain is ${v_{r/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$. Hence, the correct option is C.
Note:
Alternate method:
When the man is at rest i.e., ${v_{m/g}} = 0$ , the actual velocity of the rain given by equation (1) is ${\vec v_{r/g}} = {v_x}\hat i + {v_y}\hat j$ where ${v_x}$ and ${v_y}$ are the components of the velocity in the x-direction and y-direction respectively.
Since the angle made by the velocity of the raindrops with the horizontal is $60^\circ $ ,$\tan 60^\circ = \dfrac{{{v_y}}}{{{v_x}}} = \sqrt 3 $
$ \Rightarrow {v_y} = \sqrt 3 {v_x}$ ----------- (A)
When the man moves with a velocity of ${v_{m/g}} = 5{\text{km}}{{\text{h}}^{ - 1}}$ in the horizontal direction, the actual velocity of the rain given by equation (1) is ${\vec v_{r/g}} = \left( {5 + {v_x}} \right)\hat i + {v_y}\hat j$
Here, the angle made by the velocity of the raindrops with the horizontal is $30^\circ $.
So, $\tan 30^\circ = \dfrac{{{v_y}}}{{5 + {v_x}}} = \dfrac{1}{{\sqrt 3 }}$
$ \Rightarrow \sqrt 3 {v_y} = 5 + {v_x}$ ------------ (B)
From equations (A) and (B) we get, $3{v_x} = 5 + {v_x}$ or ${v_x} = \dfrac{5}{2}$
And then ${v_y} = \dfrac{{5\sqrt 3 }}{2}$
So the resultant velocity will be ${v_{r/g}} = \sqrt {{{\left( {\dfrac{5}{2}} \right)}^2} + {{\left( {\dfrac{{5\sqrt 3 }}{2}} \right)}^2}} = 5{\text{km}}{{\text{h}}^{ - 1}}$
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




