Question

A man is coming down an incline of angle \[{{30}^{0}}\], When he walks with speed \[2\sqrt{3}\]m/s he has to keep his umbrella vertical to protect himself from rain. The actual speed of rain is 5m/s. At what angle with vertical should he keep his umbrella when he is at rest so that he does not get drenched?

Answer 1

Hint: In this problem we have to use vector algebra in order to find out the desired angle. The rain is falling vertically downwards and the man is walking on an inclined plane at an angle of \[{{30}^{0}}\]. The velocity vector of the man and the velocity vector of the rain can be added vectorially in order to find the resultant vector.

Complete step by step answer:
We find the velocity of rain with respect to rain.

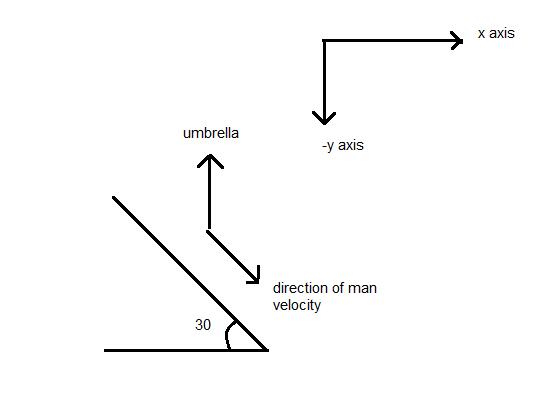
Since the angle between the velocity vector and the rain is not perpendicular, hence, the umbrella should be held tilted at some angle with respect to vertical.
Horizontal component of velocity vector,
$
 v\cos 30=\dfrac{\sqrt{3}}{2}\times 2\sqrt{3} \\
 \Rightarrow 3m{{s}^{-1}} \\
$
And the vertical component is \[v\sin 30=\dfrac{1}{2}\times 2\sqrt{3}=\sqrt{3}m{{s}^{-1}}\]
Let the angle that umbrella made with the vertical be \[\alpha \]
Velocity of rain with respect to the man can be given as: \[{{\overrightarrow{v}}_{RM}}={{\overrightarrow{v}}_{R}}-{{\overrightarrow{v}}_{M}}\]
\[\Rightarrow 5\{\sin \alpha \widehat{i}+\cos \alpha \widehat{j\}}-(3\widehat{i}-\sqrt{3}\widehat{j})\]
$
\Rightarrow 5\sin \alpha -3=0 \\
 \Rightarrow \alpha ={{\sin }^{-1}}(\dfrac{3}{5}) \\
 \therefore \alpha ={{37}^{0}} \\
$
so when man is at rest then he must have to hold his umbrella at 37 degree with the vertical

Note:
We have resolved the vector in order to find the resultant direction. Here we have put the vertical component equal to zero because the umbrella is making angle with the vertical and not with the horizontal, thus we put the horizontal component of the resultant velocity equivalent to 0.