Question

A man has to go $50m$ due north, $40m$ due east and $20m$ due south to reach a field.
(A). what is the distance he has to walk to reach the field.
(B). what is his displacement from his house to the field?

Answer 1

Hint: The four main directions are: north, south, east, and west. Distance is the path taken between two points while displacement is the shortest path between two points. We can calculate the distance by adding the length of the paths the man travelled in all directions, while for displacement, we can calculate the line joining both points.

Formula used:
$H{{F}^{2}}=A{{H}^{2}}+A{{F}^{2}}$

Complete step-by-step solution:
Let the man follow the path as follows-

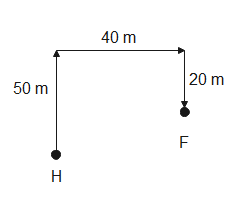
The distance is the length of the path taken by the man to reach the field from his home. The length of the path is-
$\begin{align}
  & l=50+40+20 \\
 & \therefore l=110m \\
\end{align}$

The total distance that the man travels is $110m$.

Displacement is the shortest distance between two points. It has magnitude as well as direction. While displacement is a vector, distance is a scalar.

The displacement between the man’s home and field will be-

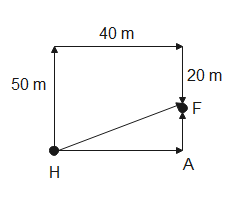
In triangle HAF,
$\begin{align}
  & AH=40m \\
 & AF=50-20=30m \\
\end{align}$

Applying Pythagoras theorem in $\Delta HAF$
$\begin{align}
  & H{{F}^{2}}=A{{H}^{2}}+A{{F}^{2}} \\
 & \Rightarrow H{{F}^{2}}={{(40)}^{2}}+{{(30)}^{2}} \\
 & \Rightarrow H{{F}^{2}}=2500 \\
 & \therefore HF=50m \\
\end{align}$

Therefore, the displacement between the man’s house and field is $50m$.

Therefore, the distance travelled by the man is $110m$, while the displacement between two points is $50m$.

Additional information:
There are different equations which are used to describe the motion of an object in one direction. They give us a relation between initial and final velocity, acceleration, displacement and time taken by an object. These are- $v=u+at$, ${{v}^{2}}={{u}^{2}}+2as$, $s=ut+\dfrac{1}{2}a{{t}^{2}}$.

Note:
The displacement is always shorter than the distance. Its direction is in the direction of motion of the object. Distance describes the motion of an object in one- dimension while displacement describes it in two-dimensions. Displacement is fundamental to other parameters like velocity and acceleration which describe motion.