Question

A man $2m$ high walk at a uniform speed of $5\dfrac{m}{{\min }}$ away from the lamppost $5m$ high. Find the rate at which length of its shadow increases.

Answer 1

Hint:Draw the diagram to solve this type of problem. As you go away from any source of light then your shadow will increase at the same rate. From the diagram determine tangent function, equate the values and differentiate it, then we get the required answer.

Complete step-by-step answer:
First of all let’s draw the diagram. Since there is a lamppost, let $AB$ which is $5m$ high and let man be represented by $MN$ whose height is $2m$.

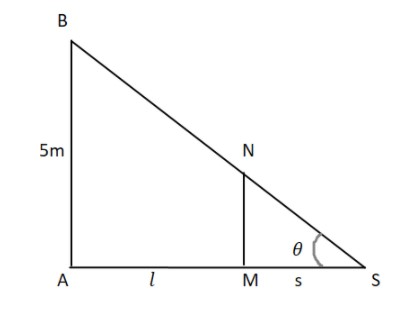
Here $MS$ is the shadow of the man $MN$. So let us suppose currently $AM = l\,meter$ that means the man is $l\,meter$ apart from the lamppost $AB$
Here $MS$ is the shadow and let the length of shadow be $s$
$MS = s$
And given in the question that man walks away from the lamppost with speed of $5\dfrac{m}{{\min }}$. If man walks towards right then the length between lamppost and man also increase with time i.e.
$\dfrac{{dl}}{{dt}} = \;5\dfrac{m}{{\min }}$and as he moves, the shadow length also starts increasing with rate=$\dfrac{{ds}}{{dt}}$
Now in $\Delta ASB$ we know that
$
  \tan \theta = \dfrac{{perpendicular}}{{base}} \\
  \tan \theta = \dfrac{{AB}}{{AS}} = \dfrac{5}{{l + s}} \\
 $
Now in $\Delta MSN$, we know
 \[\tan \theta = \dfrac{{NM}}{{MS}} = \dfrac{2}{s}\]
So both are equal to $\tan \theta $,
$
  \dfrac{5}{{l + s}} = \dfrac{2}{s} \\
  5s = 2l + 2s \\
  3s = 2l \\
  l = \dfrac{{3s}}{2} \\
 $
If we differentiate with respect to time we get
$\dfrac{{dl}}{{dt}} = \dfrac{3}{2}\dfrac{{ds}}{{dt}}$
Now we are given that $\dfrac{{dl}}{{dt}} = 5\dfrac{m}{{\min }}$
\[
  \therefore \,5 = \dfrac{3}{2}\dfrac{{ds}}{{dt}} \\
  \dfrac{{ds}}{{dt}} = \dfrac{{10}}{3}\,\dfrac{m}{{\min }} \\
 \]
Hence we can say that the rate of increase of shadow length is $\dfrac{{10}}{3}\,\dfrac{m}{{\min }}$

Note:Here the rate of increase of shadow length is also treated as the velocity or speed of shadow. The rate of change in length with time gives the speed.Students should know trigonometric ratios formula for solving these types of questions.