Question

A man 1.8 m tall stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4m on the ground. Find the height of the lamp post.
$
  (a){\text{ 2m}} \\
  (b){\text{ 5m}} \\
  (c){\text{ 3m}} \\
  (d){\text{ 7m}} \\
$

Answer 1

Hint – In this question consider CD as the height of man and AB as the height of the tower (see figure). Use $\tan \theta $ in triangle ABE and triangle CDE, to get the relation between the heights and the length of shadows cast. This will help getting the answer.

Complete step-by-step answer:

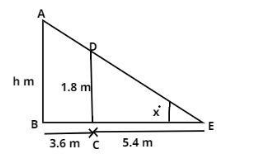
Let AB be the lamp post whose height be (h) meter as shown in figure.
Let DC be the man standing at 3.6 meter from the lamp post whose height is 1.8 meter as shown in figure.
The CE is the shadow of the man whose length is 5.4 meter as shown in figure.
So in triangle CDE, let $\angle CED = {x^ \circ }$ and we all know that tan is the ratio of perpendicular to base so we have,
$ \Rightarrow \tan {x^ \circ } = \dfrac{{CD}}{{CE}} = \dfrac{{1.8}}{{5.4}} = \dfrac{1}{3}$
Now in triangle ABE we have,
$ \Rightarrow \tan {x^ \circ } = \dfrac{{AB}}{{BE}} = \dfrac{h}{{BC + CE}}$
Now substitute the values we have,
$ \Rightarrow \dfrac{1}{3} = \dfrac{h}{{3.6 + 5.4}}$
$ \Rightarrow \dfrac{1}{3} = \dfrac{h}{9}$
$ \Rightarrow h = \dfrac{9}{3} = 3$ meter.
So the height of the lamp post is 3 meter.
So this is the required answer.
Hence option (C) is correct.

Note – Diagrammatic representation using the information provided in the question always helps in understanding the basic geometry of the problems. It is always advised to remember the direct formula for basic trigonometric ratios just like tan is the ratio of perpendicular and base. Key point here is that in such height and distance based problems the trigonometric ratio of $\tan \theta $ is most frequently used, so align the line of thought in this direction only while solving problems of this kind.