Question

A long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the center of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the center of this coil of n turns will be.
$
  (a){\text{ 2}}{{\text{n}}^2}B \\
  (b){\text{ nB}} \\
  {\text{(c) }}{{\text{n}}^2}B \\
  (d){\text{ 2n = B}} \\
$

Answer 1

Hint: Let the initial length of the wire be x cm and since it is converted into a coil so the circumference of the coil must be equal to length of the long wire. Use the direct formula that the magnetic field at the center of the coil is $B = \dfrac{{{\mu _o}I}}{{2R}}$. Now since the same wire is bent into a circular coil of n turns, so n times the circumference of this coil is equal to the circumference of the coil which is bent earlier. Use this concept to get the right answer.

Complete step-by-step solution -

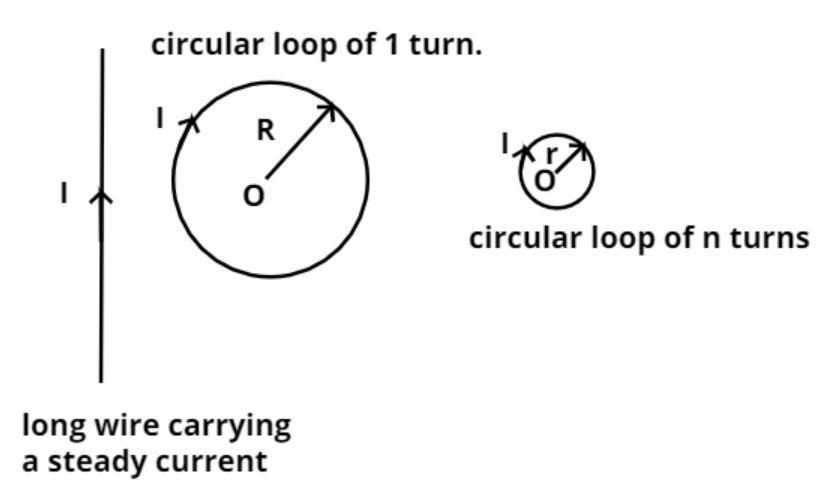
Let the length of the long wire be X cm.
Now this wire is converted into a circular coil of 1 turn as shown in the figure, where O is the center of the circle.
So the circumference of the coil = length of the long wire.
$ \Rightarrow 2\pi R = X$
Now as we know that the magnetic field at the center of the coil is $B = \dfrac{{{\mu _o}I}}{{2R}}$........... (1),
Where, B = magnetic field at the center.
              I = current in the coil
              R = radius of the coil
             ${\mu _o}$ = permeability of the free space.
Now the same wire is bent into a circular coil of n turns, so n times the circumference of this coil is equal to the circumference of the coil which is bent earlier.
Let the radius of the circular coils be r cm.
$ \Rightarrow n \times 2\pi r = 2\pi R$
$ \Rightarrow r = \dfrac{R}{n}$.................... (2)
Now the magnetic field at the center of these n turns’ circular coils is
Let the magnetic field at the center of these n turns’ circular coils be B’
$ \Rightarrow B' = n\dfrac{{{\mu _o}I}}{{2r}}$
Now from equation (2) we have,
$ \Rightarrow B' = n\dfrac{{{\mu _o}I}}{{2\dfrac{R}{n}}} = {n^2}\dfrac{{{\mu _o}I}}{{2R}}$
Now from equation (1) we have,
$ \Rightarrow B' = {n^2}B$
So the new magnetic field is ${n^2}$ times the precious magnetic field.
Thus the magnetic field at the center of this coil of n turns is ${n^2}B$
So this is the required answer.
Hence option (C) is the correct answer.

Note: It is advised to remember the basic formula for the magnetic field due to a coil carrying current. The trick point here was that once this circular coil of one turn is converted into coils of n turns then the magnetic field becomes n times that of the magnetic field at the center of the coil of one turn.