Question

A long wire carrying a current $ i $ is bent to form a plane angle $ \alpha $ Find the magnetic field $ B $ at a point on the bisector of this angle situated at a distance $ x $ from the vertex.

Answer 1

Hint: We are asked to find the magnetic field at a point. To understand the question better, we can start to answer this question by drawing a diagram. We can use Biot-Savart’s law to find the magnetic field at the upper or lower part of the bent wire and multiply it to find the final solution. We also used many mathematical formulas (trigonometric) to simplify the equations as we go forward.
The magnetic field is given by the Biot-Savart’s law as $ B = \dfrac{{{\mu _0}i}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right) $

Complete Step By Step Answer:
Let us start to answer this question by drawing a diagram to understand it better

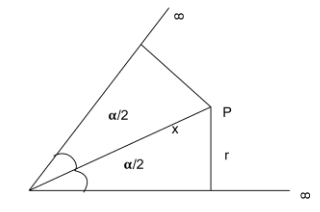
Now that we have the diagram let us move onto finding the magnetic field at the point P due to the upper and lower infinite long wires.
By the Biot-Savart’s law we have $ B = \dfrac{{{\mu _0}i}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right) $
We know that $ \sin \dfrac{\alpha }{2} = \dfrac{r}{x} $ or $ r = x\sin \dfrac{\alpha }{2} $
We also have $ {\theta _1} = \dfrac{\alpha }{2} $ and $ {\theta _2} = 90 $
The magnetic field thus becomes $ B = \dfrac{{{\mu _0}i}}{{4\pi }}\left( {\dfrac{{\sin \dfrac{\alpha }{2} + \sin 90}}{{x\sin \dfrac{\alpha }{2}}}} \right) $
This is the magnetic field at the upper or lower side, we multiply it with two and get
 $ B = \dfrac{{{\mu _0}i}}{{2\pi }}\left( {\dfrac{{\sin \dfrac{\alpha }{2} + \sin 90}}{{x\sin \dfrac{\alpha }{2}}}} \right) $
After further simplification, we have $ B = \dfrac{{{\mu _0}i}}{{2\pi x}}\left( {\dfrac{{\sin \dfrac{\alpha }{2} + 1}}{{\sin \dfrac{\alpha }{2}}}} \right) = \dfrac{{{\mu _0}i}}{{2\pi x}}\left( {\dfrac{{{{\left( {\sin \dfrac{\alpha }{4} + \cos \dfrac{\alpha }{4}} \right)}^2}}}{{2\sin \dfrac{\alpha }{4}\cos \dfrac{\alpha }{4}}}} \right) $
We use two trigonometric formulas to simplify the above equation and get the final answer. These trigonometric formulas are
(i) $ \sin 2\theta = 2\sin \theta \cos \theta $
(ii) $ 1 + \sin \theta = {\left( {\sin \dfrac{\theta }{2} + \cos \dfrac{\theta }{2}} \right)^2} $
We divide both the denominator and numerator by $ {\cos ^2}\dfrac{\alpha }{4} $ and we get
 $ B = \dfrac{{{\mu _0}i}}{{2\pi x}}\left( {\dfrac{{{{\left( {1 + \tan \dfrac{\alpha }{4}} \right)}^2}}}{{\tan \dfrac{\alpha }{4}}}} \right) = \dfrac{{{\mu _0}i}}{{2\pi x}}\left( {1 + \tan \dfrac{\alpha }{4}} \right)\cot \dfrac{\alpha }{4} $
The final answer for the magnetic field will be $ B = k\cot \dfrac{\alpha }{4} $
Where k is $ \dfrac{{{\mu _0}i}}{{2\pi x}}\left( {1 + \tan \dfrac{\alpha }{4}} \right) $ .

Note:
The trigonometric formulas used here are the key factor one should notice. Moving onto the magnetic field, it is the vector field that gives us the influence of magnetism on moving charges and magnetic materials.