Question

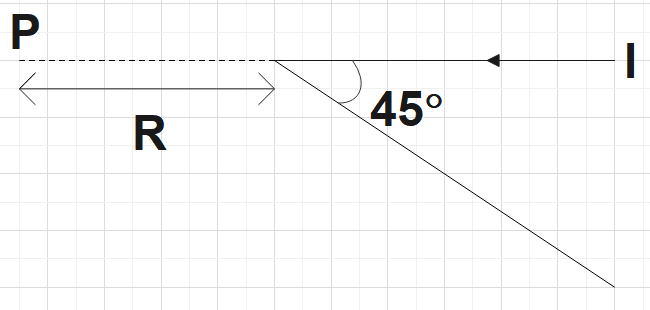
A long straight wire carrying current I is bent at its midpoint to form an angle of $45{}^\circ $ induction of magnetic field at point P distant R from point of bending is equal to:

A. $\dfrac{\left( \sqrt{2}-1 \right){{\mu }_{0}}I}{4\pi R}$
B. $\dfrac{\left( \sqrt{2}+1 \right){{\mu }_{0}}I}{4\pi R}$
C. $\dfrac{\left( \sqrt{2}+1 \right){{\mu }_{0}}I}{4\sqrt{2}\pi R}$
D. $\dfrac{\left( \sqrt{2}-1 \right){{\mu }_{0}}I}{2\sqrt{2}\pi R}$

Answer 1

Hint: As a first step, one could read the question well and hence note down the given points carefully. Then you could recall the expression for magnetic field induction as per the given conditions in the question. Then carry out the substitutions accordingly to find the answer.

Formula used:
Magnetic field induction,
$B=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)$

Complete step-by-step solution:
In the question, we are given a long straight wire that is carrying current I that is bent at its midpoint forming a $45{}^\circ $angle. We are supposed to find the magnetic field induction at point P that is at a distance R from this point of bending.
Let us recall the expression for magnetic induction given by,
$B=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)$…………………………………………. (1)
From the given figure, $d=R\cos 45{}^\circ $
Also, ${{\phi }_{1}}=-{{45}^{0}}$and ${{\phi }_{2}}=90{}^\circ $
One could substitute these values into equation (1) to get,
$B=\dfrac{{{\mu }_{0}}I}{4\pi R\cos 45{}^\circ }\left( \sin \left( -45{}^\circ \right)+\sin 90{}^\circ \right)$
Substituting the sine and cosine of these angles, we would get,
$\Rightarrow B=\dfrac{{{\mu }_{0}}I\sqrt{2}}{4\pi R}\left( 1-\dfrac{1}{\sqrt{2}} \right)$
$\therefore B=\dfrac{\left( \sqrt{2}-1 \right){{\mu }_{0}}I}{4\pi R}$
Therefore, we found the magnetic field induction at the point P due to the given bend wire would be, $B=\dfrac{\left( \sqrt{2}-1 \right){{\mu }_{0}}I}{4\pi R}$
Hence, option A is found to be correct.

Note: We could define electromagnetic or magnetic induction as the production of an electromotive force across an electrical conductor in the vicinity of varying magnetic fields. The man behind the discovery of induction is Michael Faraday and it was mathematically described by maxwell.