Question

A long solenoid is formed by winding $20\,turns\,c{m^{ - 1}}$. What will be the current necessity to produce a magnetic field of $20mT$ inside the solenoid ($\dfrac{{{\mu _0}}}{{4\pi }} = {10^{ - 7}}metre$$Amper{e^{ - 1}}$)
(A) $8.0A$
(B) $4.0A$
(C) $2.0A$
(D) $1.0A$

Answer 1

Hint:We are asked to find the current needed that would produce a magnetic field of magnitude $20mT$ inside the solenoid. In order to proceed, you need to find the magnetic field inside a current carrying solenoid in terms of current and the number of turns per centimetre and from there you can easily find the value of current.

Complete step by step answer:
A solenoid is a wire which is wound closely in the form of helix. Let us first look at the cross section of a solenoid.

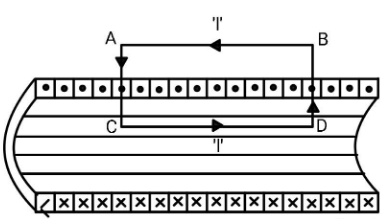
Here, the cross indicates that the current is flowing inside, away from you and the dot indicates that the current is flowing outside, towards you.There will be two kinds of magnetic field, one will be parallel to side AB and the other one will be parallel to side BD. The magnetic field parallel to side BC will be zero because there will be similar adjacent loops which will cancel this magnetic field. Now, we are left with only the magnetic fields which are parallel to side AB.

Consider Ampere’s Law which is given as $\oint {{\mathbf{B}}.{\mathbf{dl}}} = {\mu _0}{I_{enc}}$. Due to symmetry, the magnetic field at any point which lies on line CD will be equal and so is with the line AB. Let the magnetic field on line AB be ${B_2}$ and that on line CD be ${B_1}$, according to Ampere’ law, for loop ACDB, ${B_2}l - {B_1}l = {\mu _0}NI \to {B_1}l = {B_2}l - {\mu _0}NI$. Now, if we extend the lines BD and AC to infinity, we will get another loop and then we will have ${B_1}l = {B_{_{infinity}}}l - {\mu _0}NI$.

From here, we can say that the magnetic field just outside the solenoid and at infinity will be the same. As you know that the magnetic field is inversely proportional to the distance, it will be zero at infinity and so will it be just outside the solenoid. For, a solenoid, the Ampere’s law will be ${B_1} = {B_{inside}} = - \dfrac{{{\mu _0}NI}}{l} = {\mu _0}nI$, where $n = \dfrac{N}{l}$ is the number of turns per metre. The negative sign indicates that the magnetic field will be in the opposite direction and hence we can ignore it.
${B_{inside}} = {\mu _0}nI$.
$\Rightarrow I = \dfrac{{{B_{inside}}}}{{{\mu _0}n}}$. Substituting the values, we get,
$\therefore I = \dfrac{{\left( {20 \times {{10}^{ - 3}}} \right)}}{{\left( {4\pi \times {{10}^{ - 7}}} \right)\left( {20 \times {{10}^2}} \right)}} \approx 8.0A$
Therefore, the current necessity to produce a magnetic field of $20mT$ inside the solenoid will be $8.0A$.

Hence, option A is correct.

Note: Keep in mind the method we used to derive the magnetic field inside the solenoid. The magnetic fields parallel to the side BD are cancelled out by adjacent loops and add up to zero and the magnetic field outside the solenoid is zero. Also keep in mind to convert the units of the quantities appropriately. It is a good habit to keep track of units every time while solving any question.