Question

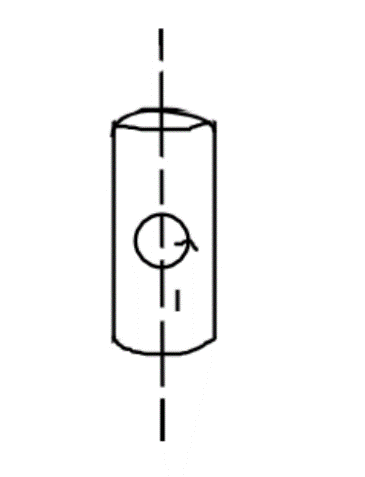
A long circular tube of length 10m and radius 0.3 m carries a current I along its curved surface area as shown. A wire-loop of resistance 0.005ohms and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $I = {I_o}\cos \left( {300t} \right)$ where ${I_o}$ is constant, if the magnetic moment of the loop is $N{\mu _o}{I_o}\sin \left( {300t} \right)$ then ‘N’ is

Answer 1

Hint: In this question use the concept that the circular wire loop placed inside the long circular tube will behave as a solenoid, so use the direct formula for the magnetic field due to a solenoid that is $B = {\mu _o}nI$. Use the concept of magnetic flux that is $\phi = BA$, along with the Lenz law $e = - \dfrac{{d\phi }}{{dt}}$, this will help approaching the solution of this problem.

Complete step-by-step answer:
Given data:
Length of long circular tube = 10m
Radius of the long circular tube = 0.3m
Carries a current I along its curved surface as shown in the figure.
Now a wire-loop is placed inside the tube with its axis coinciding with the axis of the tube.
Having loop resistance R = 0.005 Ohm
And radius (r) of the loop = 0.1m
The current varies as $I = {I_o}\cos \left( {300t} \right)$, where ${I_o}$ is constant.
Now if the magnetic moment of the loop is $N{\mu _o}{I_o}\sin \left( {300t} \right)$................. (1)
So we have to find the value of N.
Now as we know that the magnetic field generated in the solenoid (circular ring behaves as a solenoid)
$ \Rightarrow B = {\mu _o}nI$
Where, ${\mu _o} = $permeability of the free space
               n = number of turns per unit length = ($\dfrac{{N'}}{L}$)
   $ \Rightarrow B = {\mu _o}nI = {\mu _o}\dfrac{{N'I}}{L}$
Here $N' = 1$ as there is only a single circular turn.
$ \Rightarrow B = {\mu _o}\dfrac{I}{L}$
Now the flux passing through the circular coil is given as
$ \Rightarrow \phi = BA$, where $\phi $ = magnetic flux, A = area of the circular loop = $\pi {r^2}$
$ \Rightarrow \phi = {\mu _o}\dfrac{I}{L}\left( {\pi {r^2}} \right)$
Now according to Lenz law induced e.m.f in the coil is
$ \Rightarrow e = - \dfrac{{d\phi }}{{dt}}$
Now substitute the value we have,
$ \Rightarrow e = - \dfrac{d}{{dt}}\left( {{\mu _o}\dfrac{I}{L}\left( {\pi {r^2}} \right)} \right)$
Now in the above equation only I is variable and remaining all things are constant w.r.t time so we have,
$ \Rightarrow e = - \dfrac{{{\mu _o}\pi {r^2}}}{L}\dfrac{{dI}}{{dt}}$
Now the induced current (i) in the coil according to ohm's law we have,
$ \Rightarrow i = \dfrac{e}{R}$, where R = resistance of the coil.
$ \Rightarrow i = - \dfrac{{{\mu _o}\pi {r^2}}}{{LR}}\dfrac{{dI}}{{dt}}$
Now the magnetic moment (M) of the coil is the product of the induced current (i) and the area (A) of the coil so we have,
$ \Rightarrow M = iA$
Now substitute the values we have,
$ \Rightarrow M = - \dfrac{{{\mu _o}\pi {r^2}}}{{LR}}\dfrac{{dI}}{{dt}}\left( {\pi {r^2}} \right)$
$ \Rightarrow M = - \dfrac{{{\mu _o}{\pi ^2}{r^4}}}{{LR}}\dfrac{{dI}}{{dt}}$
Now the current is varying as $I = {I_o}\cos \left( {300t} \right)$
$ \Rightarrow M = - \dfrac{{{\mu _o}{\pi ^2}{r^4}}}{{LR}}\dfrac{d}{{dt}}\left( {{I_o}\cos \left( {300t} \right)} \right)$
Now differentiate it according to rule $\dfrac{d}{{dt}}\cos wt = - w\sin wt$ so we have,
$ \Rightarrow M = 300\dfrac{{{\mu _o}{\pi ^2}{r^4}}}{{LR}}\left( {{I_o}\sin \left( {300t} \right)} \right)$
$ \Rightarrow M = 300\dfrac{{{\pi ^2}{r^4}}}{{LR}}{\mu _o}{I_o}\sin \left( {300t} \right)$
Now compare this equation from equation (1) we have,
$ \Rightarrow M = N{\mu _o}{I_o}\sin \left( {300t} \right) = 300\dfrac{{{\pi ^2}{r^4}}}{{LR}}{\mu _o}{I_o}\sin \left( {300t} \right)$
So on comparing we have,
$ \Rightarrow N = 300\dfrac{{{\pi ^2}{r^4}}}{{LR}}$
Now substitute the values we have,
$ \Rightarrow N = 300\dfrac{{{{\left( {\dfrac{{22}}{7}} \right)}^2}{{\left( {0.1} \right)}^4}}}{{10 \times 0.005}}$
Now simplify this we have,
$ \Rightarrow N = 0.6{\left( {\dfrac{{22}}{7}} \right)^2} = 5.926 \simeq 6$
So this is the required answer.

Note – A solenoid is simply a coil of wire carrying current. It is in the cylindrical form and has turns associated with it. The magnetic field produced due to this solenoid is directly affected by the number of turns present in that solenoid. The trick part of this problem was understanding why the cylindrical coil and circular wire assembly is taken as solenoid.