Question

A load of mass m falls from a height h on the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is K and the mass of the scale pan is zero and the mass m does not bounce relative to the pan, then what will be the amplitude of the vibration of the pan and mass?

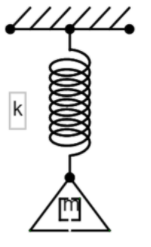
Answer 1

Hint: The amplitude of vibration can be derived from the equation of simple harmonic motion. Since the pan is massless and the vibration is uniform, the equation can be directly substituted from the Hooke’s law and potential energy at a height.
Formula Used:
The energy of spring from Hooke’s law: \[{{E}_{h}}=\dfrac{1}{2}k{{x}^{2}}\]
The potential energy of a mass ‘m’ at height ‘h’ is mgh.

Complete answer:
We can understand from the diagram that the mass is falling from a height ‘h’ to the spring pan. The mass by virtue of its height has a potential energy. Also, once the mass touches the pan the spring elongates and an energy is stored due to this. Both the energy should be balancing for a smooth vibration. So, let us consider the equation of balancing energies –
  

  \[\begin{align}
  & mg(h+x)=\dfrac{1}{2}k{{x}^{2}} \\
 & \Rightarrow 2mgh+2mgx=k{{x}^{2}} \\
 & \Rightarrow k{{x}^{2}}-2mgx-2mgh=0 \\
 & \Rightarrow k{{x}^{2}}-2mgx=2mgh \\
 & \Rightarrow {{x}^{2}}-\dfrac{2mgx}{k}=\dfrac{2mgh}{k} \\
\end{align}\]
Now applying the equation for solving the quadratic equation,
\[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\]
\[x=\dfrac{-(-\dfrac{2mg}{k})\pm \sqrt{{{(\dfrac{-2mg}{k})}^{2}}-4\times 1\times \dfrac{-2mgh}{k}}}{2}\]
Reducing this to the simplest form gives the amplitude of the vibration, we take the common two from the square root and cancel it with the denominator. Afterwards, we take the whole \[\dfrac{mg}{k}\]factor out of the square root. And gets the answer.
\[\Rightarrow x=\dfrac{mg}{k}\pm \sqrt{\dfrac{mg}{k}(\dfrac{mg}{k}+2h)} \]
\[\Rightarrow x=\dfrac{mg}{k}\pm \dfrac{mg}{k}\sqrt{1+\dfrac{2kh}{mg}} \]

This gives the amplitude of vibration of the mass together with the pan.
Now, at the equilibrium condition \[mg=kx{}_{0}\]
\[\Rightarrow {{x}_{0}}=\pm \dfrac{mg}{k}\sqrt{1+\dfrac{2kh}{mg}}\]
This is the amplitude of vibration at the equilibrium.

Note:
We have considered the vibration such that there is no damping effect involved. We can use a simple harmonic equation if the frequency is relevant in the question. The spring constant plays an important role in determining the amplitude of the system.