
A line which touches both ${{y}^{2}}-8x=0$ and ${{x}^{2}}+{{y}^{2}}+8x+14=0$ is
(a) $x+y+2=0$
(b) $x+y-2=0$
(c) $x-y+2=0$
(d) $x-y-2=0$
Answer
603.6k+ views
Hint: Proceed by first writing the general equation of the tangent of a parabola, which is $y=mx+\dfrac{a}{m}$, and then making this tangent satisfy the condition for being a tangent to the circle. For this, the tangent should be perpendicular to the radius at the point where the tangent touches the circle, and it’s perpendicular distance from the centre should be equal to the circle’s radius.
Complete step-by-step solution -
The equation ${{y}^{2}}-8x=0$ is the equation of a parabola. Let’s call this parabola ${{P}_{1}}$.
The general form of a parabola is : ${{y}^{2}}=4ax$ whose coordinates of vertex $=(0,0)$and the coordinates of its focus $=(a,0)$.
Comparing the general form of the equation of a parabola to the equation of ${{P}_{1}}$, we get :
$\begin{align}
& 4ax=8x \\
& \Rightarrow 4a=8 \\
& \Rightarrow a=2 \\
\end{align}$
Hence, ${{P}_{1}}$ is a parabola with its vertex at $(0,0)$ and its focus at $(2,0)$.
The equation ${{x}^{2}}+{{y}^{2}}+8x+14=0$ clearly is the equation of a circle since it matches the general form of the equation of a circle which is :
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where the circle’s centre is $(-g,-f)$and its radius is equal to $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Let’s call the equation ${{x}^{2}}+{{y}^{2}}+8x+14=0$ the equation of a circle ${{S}_{1}}$.
Comparing ${{S}_{1}}$to the general form of a circle, we get :
$\begin{align}
& 2gx=8x \\
& \Rightarrow 2g=8 \\
& \Rightarrow g=4 \\
\end{align}$
And,
$\begin{align}
& 2fy=0 \\
& \Rightarrow 2f=0 \\
& \Rightarrow f=0 \\
\end{align}$
Hence, for the circle ${{S}_{1}}$, its centre ${{C}_{1}}$$=(-g,-f)=(-4,0)$
And its radius ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{4}^{2}}-14}=\sqrt{2}$
To find a line that touches both, the parabola ${{P}_{1}}$ and the circle ${{S}_{1}}$, we need to find a common tangent between the two.
The general equation of a tangent of a parabola can be written as :
$y=mx+\dfrac{a}{m}$ …….(1) where $a$ is the $x$ coordinate of the focus point, since here we are dealing with parabolas whose foci have one of the coordinates as $0$.
$m$ here is the slope of the tangent, and it’s variable, since the no. of tangents that can be drawn to a parabola are infinite.
Since the question says that this tangent should touch the circle, as well, it should also act as a tangent to the circle.
And for any line to be a tangent to the circle ${{S}_{1}}$, it is mandatory that the perpendicular distance from the centre of the circle, ${{C}_{1}}$, is equal to the radius of the same circle, or ${{r}_{1}}$.
$\Rightarrow d=r_1$ where $d$ is the perpendicular distance of ${{C}_{1}}$ from line (1).
The perpendicular distance, $d$, of any point $(X,Y)$from a line $Ax+By+C=0$ can be written as :
$d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Since we know that in this case, $d=r_1$
$\Rightarrow r_1=\dfrac{|A(-g)+B(-f)+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$………………………….(2)
The line being considered here is line (1), for which :
$A=m,B=-1,C=\dfrac{a}{m}$
Substituting these values in equation (2) and substituting the coordinates of the centre of circle ${{S}_{1}}$, we get :
$\begin{align}
& r_1=\dfrac{|m(-4)+0(-1)+\dfrac{a}{m}|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow \sqrt{2}=\dfrac{|-4m+\dfrac{a}{m}|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow \sqrt{2({{m}^{2}}+1)}=|\dfrac{a}{m}-4m| \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& \Rightarrow 2({{m}^{2}}+1)={{(\dfrac{a}{m}-4m)}^{2}} \\
& \Rightarrow 2{{m}^{2}}+2=\dfrac{{{a}^{2}}}{{{m}^{2}}}+16{{m}^{2}}-8a \\
\end{align}$
Substituting the value of $a$ as $2$, which we already found out, we get :
$\begin{align}
& \Rightarrow 2{{m}^{2}}+2=\dfrac{4}{{{m}^{2}}}+16{{m}^{2}}-16 \\
& \Rightarrow 2{{m}^{2}}+18=\dfrac{4}{{{m}^{2}}}+16{{m}^{2}} \\
& \Rightarrow 2{{m}^{2}}+18=\dfrac{4+16{{m}^{4}}}{{{m}^{2}}} \\
& \Rightarrow {{m}^{2}}(2{{m}^{2}}+18)=4+16{{m}^{4}} \\
& \Rightarrow 2{{m}^{4}}+18{{m}^{2}}=4+16{{m}^{4}} \\
& \Rightarrow 14{{m}^{4}}-18{{m}^{2}}+4=0 \\
& \Rightarrow 14{{m}^{4}}-14{{m}^{2}}-4{{m}^{2}}+4=0 \\
& \Rightarrow 14{{m}^{2}}({{m}^{2}}-1)-4({{m}^{2}}-1)=0 \\
& \Rightarrow ({{m}^{2}}-1)(14{{m}^{2}}-4)=0 \\
\end{align}$
Dividing both sides by $2$, to simplify the equation, we get :
$\begin{align}
& \Rightarrow ({{m}^{2}}-1)(7{{m}^{2}}-2)=0 \\
& \Rightarrow m=\pm 1,\pm \sqrt{\dfrac{2}{7}} \\
\end{align}$
Hence, we have finally got the values of $m$ that can be substituted in equation (1) along with the value of a to get the common tangent, or the line touching both the figures.
Substituting $m=1$, we get :
$\begin{align}
& y=x+a \\
& \Rightarrow y=x+2 \\
& \Rightarrow x-y+2=0 \\
\end{align}$………………………….(3)
Substituting $m=-1$, we get :
$\begin{align}
& y=-x-a \\
& \Rightarrow y=-x-2 \\
& \Rightarrow x+y+2=0 \\
\end{align}$…………………………….(4)
Substituting $m=-\sqrt{\dfrac{2}{7}}$, we get :
$\begin{align}
& y=-\sqrt{\dfrac{2}{7}}x-a\sqrt{\dfrac{7}{2}} \\
& \Rightarrow y=-\sqrt{\dfrac{2}{7}}x-\sqrt{14} \\
& \Rightarrow \sqrt{2}x+\sqrt{7}y+7\sqrt{2}=0 \\
\end{align}$
Substituting $m=\sqrt{\dfrac{2}{7}}$, we get :
$\begin{align}
& y=\sqrt{\dfrac{2}{7}}x+a\sqrt{\dfrac{7}{2}} \\
& \Rightarrow y=\sqrt{\dfrac{2}{7}}x+\sqrt{14} \\
& \Rightarrow \sqrt{2}x-\sqrt{7}y+7\sqrt{2}=0 \\
\end{align}$
To ease your understanding, here is the illustration of P1, $S_1$ and the two tangents :
Here, eq3 and eq4 are the tangents we just found out.
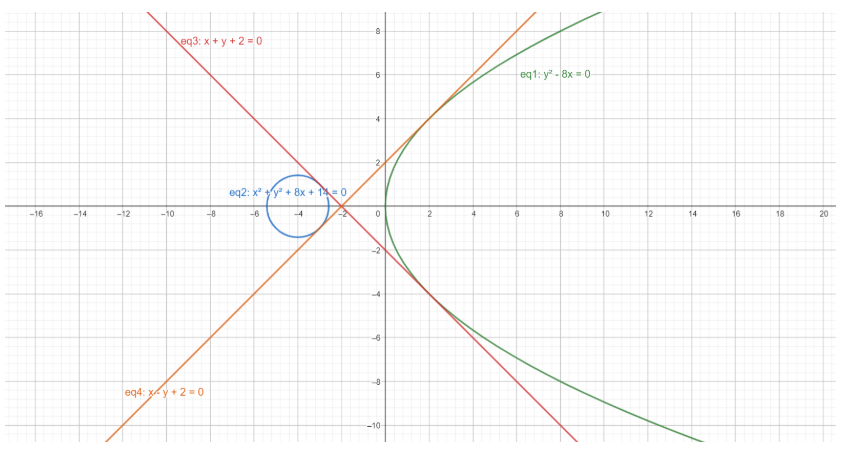
Out of the four equations obtained, equations (3) and (4) match two of the options.
Hence, the required equations are (a) and (c).
Note: Don’t use the concept of direct and transverse common tangents here, please note that direct and transverse common tangents exist only in the cases of two circles. Since, here we have one figure as a parabola, the right way would be to equate the tangent of the parabola, in the general form, for being a tangent to the circle as well.
Complete step-by-step solution -
The equation ${{y}^{2}}-8x=0$ is the equation of a parabola. Let’s call this parabola ${{P}_{1}}$.
The general form of a parabola is : ${{y}^{2}}=4ax$ whose coordinates of vertex $=(0,0)$and the coordinates of its focus $=(a,0)$.
Comparing the general form of the equation of a parabola to the equation of ${{P}_{1}}$, we get :
$\begin{align}
& 4ax=8x \\
& \Rightarrow 4a=8 \\
& \Rightarrow a=2 \\
\end{align}$
Hence, ${{P}_{1}}$ is a parabola with its vertex at $(0,0)$ and its focus at $(2,0)$.
The equation ${{x}^{2}}+{{y}^{2}}+8x+14=0$ clearly is the equation of a circle since it matches the general form of the equation of a circle which is :
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where the circle’s centre is $(-g,-f)$and its radius is equal to $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Let’s call the equation ${{x}^{2}}+{{y}^{2}}+8x+14=0$ the equation of a circle ${{S}_{1}}$.
Comparing ${{S}_{1}}$to the general form of a circle, we get :
$\begin{align}
& 2gx=8x \\
& \Rightarrow 2g=8 \\
& \Rightarrow g=4 \\
\end{align}$
And,
$\begin{align}
& 2fy=0 \\
& \Rightarrow 2f=0 \\
& \Rightarrow f=0 \\
\end{align}$
Hence, for the circle ${{S}_{1}}$, its centre ${{C}_{1}}$$=(-g,-f)=(-4,0)$
And its radius ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{4}^{2}}-14}=\sqrt{2}$
To find a line that touches both, the parabola ${{P}_{1}}$ and the circle ${{S}_{1}}$, we need to find a common tangent between the two.
The general equation of a tangent of a parabola can be written as :
$y=mx+\dfrac{a}{m}$ …….(1) where $a$ is the $x$ coordinate of the focus point, since here we are dealing with parabolas whose foci have one of the coordinates as $0$.
$m$ here is the slope of the tangent, and it’s variable, since the no. of tangents that can be drawn to a parabola are infinite.
Since the question says that this tangent should touch the circle, as well, it should also act as a tangent to the circle.
And for any line to be a tangent to the circle ${{S}_{1}}$, it is mandatory that the perpendicular distance from the centre of the circle, ${{C}_{1}}$, is equal to the radius of the same circle, or ${{r}_{1}}$.
$\Rightarrow d=r_1$ where $d$ is the perpendicular distance of ${{C}_{1}}$ from line (1).
The perpendicular distance, $d$, of any point $(X,Y)$from a line $Ax+By+C=0$ can be written as :
$d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Since we know that in this case, $d=r_1$
$\Rightarrow r_1=\dfrac{|A(-g)+B(-f)+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$………………………….(2)
The line being considered here is line (1), for which :
$A=m,B=-1,C=\dfrac{a}{m}$
Substituting these values in equation (2) and substituting the coordinates of the centre of circle ${{S}_{1}}$, we get :
$\begin{align}
& r_1=\dfrac{|m(-4)+0(-1)+\dfrac{a}{m}|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow \sqrt{2}=\dfrac{|-4m+\dfrac{a}{m}|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow \sqrt{2({{m}^{2}}+1)}=|\dfrac{a}{m}-4m| \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& \Rightarrow 2({{m}^{2}}+1)={{(\dfrac{a}{m}-4m)}^{2}} \\
& \Rightarrow 2{{m}^{2}}+2=\dfrac{{{a}^{2}}}{{{m}^{2}}}+16{{m}^{2}}-8a \\
\end{align}$
Substituting the value of $a$ as $2$, which we already found out, we get :
$\begin{align}
& \Rightarrow 2{{m}^{2}}+2=\dfrac{4}{{{m}^{2}}}+16{{m}^{2}}-16 \\
& \Rightarrow 2{{m}^{2}}+18=\dfrac{4}{{{m}^{2}}}+16{{m}^{2}} \\
& \Rightarrow 2{{m}^{2}}+18=\dfrac{4+16{{m}^{4}}}{{{m}^{2}}} \\
& \Rightarrow {{m}^{2}}(2{{m}^{2}}+18)=4+16{{m}^{4}} \\
& \Rightarrow 2{{m}^{4}}+18{{m}^{2}}=4+16{{m}^{4}} \\
& \Rightarrow 14{{m}^{4}}-18{{m}^{2}}+4=0 \\
& \Rightarrow 14{{m}^{4}}-14{{m}^{2}}-4{{m}^{2}}+4=0 \\
& \Rightarrow 14{{m}^{2}}({{m}^{2}}-1)-4({{m}^{2}}-1)=0 \\
& \Rightarrow ({{m}^{2}}-1)(14{{m}^{2}}-4)=0 \\
\end{align}$
Dividing both sides by $2$, to simplify the equation, we get :
$\begin{align}
& \Rightarrow ({{m}^{2}}-1)(7{{m}^{2}}-2)=0 \\
& \Rightarrow m=\pm 1,\pm \sqrt{\dfrac{2}{7}} \\
\end{align}$
Hence, we have finally got the values of $m$ that can be substituted in equation (1) along with the value of a to get the common tangent, or the line touching both the figures.
Substituting $m=1$, we get :
$\begin{align}
& y=x+a \\
& \Rightarrow y=x+2 \\
& \Rightarrow x-y+2=0 \\
\end{align}$………………………….(3)
Substituting $m=-1$, we get :
$\begin{align}
& y=-x-a \\
& \Rightarrow y=-x-2 \\
& \Rightarrow x+y+2=0 \\
\end{align}$…………………………….(4)
Substituting $m=-\sqrt{\dfrac{2}{7}}$, we get :
$\begin{align}
& y=-\sqrt{\dfrac{2}{7}}x-a\sqrt{\dfrac{7}{2}} \\
& \Rightarrow y=-\sqrt{\dfrac{2}{7}}x-\sqrt{14} \\
& \Rightarrow \sqrt{2}x+\sqrt{7}y+7\sqrt{2}=0 \\
\end{align}$
Substituting $m=\sqrt{\dfrac{2}{7}}$, we get :
$\begin{align}
& y=\sqrt{\dfrac{2}{7}}x+a\sqrt{\dfrac{7}{2}} \\
& \Rightarrow y=\sqrt{\dfrac{2}{7}}x+\sqrt{14} \\
& \Rightarrow \sqrt{2}x-\sqrt{7}y+7\sqrt{2}=0 \\
\end{align}$
To ease your understanding, here is the illustration of P1, $S_1$ and the two tangents :
Here, eq3 and eq4 are the tangents we just found out.

Out of the four equations obtained, equations (3) and (4) match two of the options.
Hence, the required equations are (a) and (c).
Note: Don’t use the concept of direct and transverse common tangents here, please note that direct and transverse common tangents exist only in the cases of two circles. Since, here we have one figure as a parabola, the right way would be to equate the tangent of the parabola, in the general form, for being a tangent to the circle as well.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light




